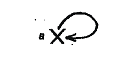Stahl,
Gerold (1997): Estructura y Conocimiento
Científico. Paidos: Buenos Aires. Capítulo I. Pp. 9-40.
CAPITULO
I
ESTRUCTURA Y CONOCIMIENTO CIENTIFICO
1. Introducción
La palabra “estructura" tiene
muchos significados diferentes, tanto en castellano como en otros idiomas. Con
un significado especial se ha transformado en término de moda, que aparece en
diversas doctrinas reunidas bajo el nombre “estructuralismo”.
Estas doctrinas filosóficas, etnológicas, lingüísticas, etc.,
además de referirse a estructuras, desarrollan
temas específicos de sus campos que a veces no tienen mucho que ver con las
estructuras. El presente análisis no se ocupa de esos temas específicos ni
entra en los detalles de las consideraciones estructuralistas propiamente tales en estos campos. Intentará, en cambio,
dar una visión general del tipo de estructuras que suelen utilizarse en matemática
y lógica matemática y extender luego estas ideas a la teoría del
conocimiento científico en general.
Dada la posicióa
señalada, es dudoso que el presente trabajo pueda calificarse de estructuralista.
Sin embargo, teniendo en cuenta que muchos estructuralistas sufrieron
la influencia directa o indirecta del término "estructura"
en el significado matemático, tal vez pueda interesar a
partidarios y opositores del estructuralismo.
Las estructuras, en el sentido en que queremos tratarlas aquí, son un tipo especial de k‑tuplo, donde por k‑tuplo se entiende una secuencia de k‑miembros, o sea, k miembros puestos en fila, uno en el primer lugar, uno en el segundo, etc., y finalmente uno en el k‑ésimo lugar. Frecuentemente los k‑tuplos se simbolizan de la siguiente manera:
<...>
colocándose en lugar de los puntos
suspensivos los símbolos
de los diferentes miembros en el orden establecido. Así el triple cuyo primer
miembro es d, el segundo a y el tercero e se simbolizaría por:
<d, a, e>
Vimos que no todos los k‑tuplos
son estructuras. Las estructuras tienen una forma muy
especial. Como primer miembro figura una clase (una colección)
que tiene por lo menos un elemento. Esta clase se
simbolizara por “V” y sus elementos se llamarán “individuos”; los individuos
en este tratamiento son objetos cualesquiera no necesariamente reales, de modo que el primer
miembro de los k‑tuplos es una colección de objetos
reales o imaginarios.
Los demás miembros de una estructura son subclases de V
o relaciones entre los elementos de V.
Conviene mencionar que hay relaciones no sólo entre dos individuos (llamadas "relaciones biposicionales"; por ejemplo: ... es el doble de. . . ) sino también entre tres individuos (llamadas “relaciones triposicionales”; ejemplo: . . . es la suma de ...y de . . . ), entre cuatro individuos, etcétera. En lugar de hablar de relaciones biposicionales, triposicionales, etc., hablaremos también de funciones proposicionales biposicionales, triposicionales, etc.
Las subclases de V, por
ejemplo todos los elementos de V que están hechos de yeso ( . . . está hecho de yeso) o todos los elementos de
V que miden menos de
En consideración de lo anterior
podemos decir que en el k‑tuplo detrás de la clase V figuran funciones
proposicionales que se refieren a los elementos de V y que pueden ser
uniposicionales o biposicionales, etc. Estas funciones
proposicionales se simbolizaran aquí por "F", “G”, "H", "K", etc., de modo
que las estructuras se simbolizarían
por:
Con todo esto ya pueden verse
algunas características del tratamiento estructural en general. Por de pronto
no se consideran objetos (individuos) aislados. Tampoco se trabaja con puras clases
o totalidades sin más; una clase V por si sola, por pobre o rica que sea en
individuos no constituye una estructura. Únicamente
si V se presenta junto con una o más funciones proposicionales, las que
a su vez se refieren exclusivamente a los individuos de V,
entonces podemos hablar de una estructura. Esta combinación
de una clase con funciones proposicionales que se refieren a los
individuos de la clase es uno de los puntos fundamentales del tratamiento estructural.
Para dar un ejemplo, consideremos
el triple cuyo primer miembro V es la clase de los números enteros (los positivos, 0 y los
negativos), F es la función proposicional
triposicional . . .
es la suma de . . y
de . . . y G es la función proposicional biposicional
. . . es el doble de . . . Vemos
que no nos interesan aquí ni determinados números enteros ni la clase de los
números enteros, sino los números enteros junto con las funciones
proposicionales de la suma y del doble, o sea todas las conexiones que rigen
entre los números enteros gracias a estas dos funciones.
En todo el tratamiento
estructural las funciones de los k‑tuplos se aplican únicamente a los individuos de la
clase V respectiva (en el ejemplo, a los números enteros). Si uno desea
trabajar con funciones proposicionales más amplias, que
además se aplican a otros individuos, no hay impedimento. Simplemente, se
forma una nueva estructura con una clase V más amplia y con funciones
proposicionales más amplias que se aplican ahora exclusivamente a los
individuos de la nueva clase V. En matemática y lógica matemática las
ampliaciones de estructuras constituyen un tema muy interesante; por ejemplo,
se desea ver cuáles características de la antigua estructura se guardan
respecto de la nueva estructura ampliada.
Ejercicio 2.1) Señalar algunas estructuras,
indicando con subíndices si las
funciones proposicionales son uniposicionales, biposicionales, etc.
Ejemplo: <est, Mod1, Pers1, Vec2, Ex2>,
donde est es es la clase de las estaciones
ferroviarias de una región; las Mod son
aquellas que están modernizadas según un criterio determinado, las otras
pertenecen automáticamente a ‑Mod; las
Pers son las que
están destinadas al transporte de personas; Vec es la relación biposicional de
vecindad entre dos estaciones y Ex la
relación biposicional de estar conectado por trenes expresos directos.
Ejercicio 2.2) Frecuentemente
se presentan estructuras con una o más relaciones de orden total (como la
relación menor entre números enteros) o de orden parcial (como la relación es divisible por entre números
enteros positivos). Indicar estructuras con relaciones de este tipo. Ejemplo: <el, Mas1, Ed2, Pes2>,
donde el es la clase de los elefantes de un
jardín zoológico; Mas son los de sexo
masculino; Ed es la relación de
tener más edad y Pes la relación de
tener más peso.
Ejercicio 2.3) Estructuras con un numero reducido
de individuos y funciones proposicionales (si éstas son sólo uniposicionales o biposicionales)
pueden presentarse de la siguiente manera: los individuos se
simbolizan por pequeñas cruces. Con signos agregados a las cruces se marca la
pertenencia a las diversas funciones uniposicionales y con flechas de diverso
tipo (flecha entera, flecha interrumpida, etc.) entre las cruces se indican
las funciones biposicionales. Representar gráficamente una estructura formada
según los ejercicios 1 o 2. Para dar un ejemplo, supongamos que haya tres
elefantes (“a”, "b", "c")
1 uno de
ellos de sexo masculino señalado "®".
La
relación Ed se representa por "®" y Pes por “‑ ‑ ‑‑>”. Podríamos tener entonces (suponiendo
que a y c sean de la misma edad, aunque no del mismo peso):
Puede
ocurrir que el individuo a esté en
relación consigo mismo (caso que se presenta siempre con la relación de
identidad, de mucha importancia en las estructuras matemáticas). Esta situación
se representa gráficamente por:
Puede ocurrir que a esté en relación F con b y viceversa
(caso que se presenta siempre con las relaciones Vec y Ex). Representación
gráfica:
Ejercicio 2.4) Para formar estructuras con individuos
de dos tipos diferentes, como personas y objetos físicos o números enteros y conjuntos de números enteros
se elige como clase V la que contiene los individuos de
las dos especies y se introduce luego una función uniposicional para hacer la
distinción entre
los individuos. Ejemplos: <pob, Pers1, . . . >, donde pob contiene personas y objetos físicos,
los Pers son
aquellos individuos que son personas (los objetos físicos serían
en este caso automáticamente ‑Pers). <enc, En1, . . . >,
donde enc contiene los números enteros y los conjuntos de números
enteros, los En son aquellos
individuos que son números enteros (los conjuntos de números enteros serían
automáticamente ‑En). Análogamente
se procede cuando hay individuos de tres o más especies. Señalar algunas
estructuras de este tipo.
Ejercicio 2.5) Frecuentemente se presentan estructuras en
que una subclase de V contiene un solo individuo. Indicar una
estructura de este tipo. Ejemplo: <enp, Baj1,
. . . >, donde enp es la clase de los números enteros
positivos y Baj es formado
por aquellos que son mas o igualmente bajos que todos (hay uno solo que, es 1).
3. Los sistemas
Para profundizar el análisis de las estructuras hay, que hablar un poco de expresiones y clases de expresiones, pues ciertas clases de expresiones están íntimamente ligadas a las estructuras.
Para
los lógicos matemáticos las expresiones no son más que secuencias de signos
tipográficos[1];
por ejemplo, la expresión “hace calor" es la letra "h”
seguida por la "a”, seguida por la "c",
seguida por la "e", seguida por el espacio
en blanco, seguida por la "c", etc. Un ejemplo
matemático sería "x+y=y+x".
Se
pueden formar clases de expresiones y algunas de estas clases que cumplen con
determinadas condiciones se llaman «sistemas». Las
expresiones que son elementos de un sistema dado se llaman
«teoremas» del sistema en cuestión. El procedimiento habitual
para formar un sistema es, en líneas generales, el siguiente: por de pronto se
descartan todas las expresiones que no se consideran
significativas para el sistema que se desea construir. En lógica matemática
esto se hace mediante reglas en forma tan rigurosa que no queda ninguna
expresión discutible, o sea, ninguna expresión de la que no se puede
determinar en forma rutinaria si es o no es significativa. Entre las
significativas respectivas que quedan hay, en los casos normales, algunas que
son teoremas del sistema y otras que no lo son. Para determinar los teoremas se
señalan algunas expresiones significativas que se llaman "teoremas básicos” o “axiomas”
del sistema. Además, por medio de ciertas reglas explícitamente señaladas se
establece
un mecanismo llamado «procedimiento demostrativo» que
permite introducir uno por uno nuevos teoremas. La clase de todos los teoremas respectivos, los básicos y los
introducidos por demostración, constituye luego el sistema en consideración.
Aunque sólo ciertos sistemas
tienen un interés practico, en
principio cualquier clase de expresiones, formada según los criterios
indicados, pero por lo demás con plena arbitrariedad, es un sistema.
Actualmente se utiliza un gran
número de sistemas, especialmente en matemática, pero también para partes de
la física, biología y economía. Entre los sistemas que tratan sectores de la
matemática hay varios que se refieren a conjuntos, otros a números naturales, a
números reales, etcétera. Hay sistemas geométricos, por ejemplo, de la
geometría euclidiana, y muchos sistemas más. Habitualmente todos
ellos se construyen de tal manera que tienen un fondo lógico común. Este fondo lógico
a su vez constituye un sistema que se llama “sistema funcional básico”.
En las expresiones de los
sistemas mencionados figuran ciertos signos o secuencias de signos que se
llaman "símbolos”. De interés especial para
lo que sigue son los símbolos
individuales que simbolizan individuos determinados (se refieren a
individuos determinados) y los símbolos funcionales
(simbolizan funciones proposicionales determinadas).
4. Modelos y
sistemas apropiados
Tomando como base las secciones
anteriores puede señalarse ahora una conexión fundamental entre sistemas y
estructuras. Para ello conviene proceder en dos etapas.
Primera etapa: tengamos, por un
lado, un sistema S. Sea C la clase de todos los símbolos individuales que
figuran en las expresiones S. Supongamos, además, que en las expresiones de S
figuran sólo (con muchas repeticiones) dos símbolos funcionales, uno de
función proposicional uniposicional y uno de función proposicional
triposicional. Tengamos, por otro lado, una estructura E,
por ejemplo <V, F, G> con F uniposicional y G triposicional.
Ahora hacemos corresponder a cada símbolo individual de C un individuo de V,
al símbolo funcional uniposicional la función F y al símbolo funcional
triposicional la función G. Esta correspondencia podría considerarse como un
tipo de simbolización o denotación, de
modo que los símbolos individuales de C simbolizarían ciertos individuos de V y
los símbolos funcionales, las funciones F
y G.
Resumiendo, tenemos por un lado
un sistema, una entidad que puede considerarse como algo lingüístico,
y por otro, una estructura, algo que normalmente no tiene nada de lingüístico.
Tenemos, por un lado, símbolos individuales y funcionales, y por otro,
individuos y funciones. Finalmente hemos logrado establecer un tipo de
relación de simbolización entre los símbolos, por un
lado, y los individuos y funciones proposicionales, por otro.
La relación de simbolización
puede establecerse sólo si la estructura E es lo suficientemente rica;
es decir, si en el sistema S hay símbolos funcionales
n‑posicionales,
debe haber, en la estructura E por lo menos una
función proposicional n‑posicional. Esta exigencia es bien razonable,
pues de otro modo ¿a que función de E se refiere el símbolo funcional?
En cambio no se exige que diferentes símbolos individuales o funcionales
simbolicen siempre diferentes individuos
o funciones; es perfectamente admisible que, por ejemplo, "IV" y “4" simbolicen
un mismo individuo, y lo mismo ocurre con
las funciones
proposicionales. Aunque así dos o mas símbolos pueden simbolizar lo
mismo, sin embargo, un símbolo del sistema que se considera simboliza un solo
individuo o una sola función de una estructura, de modo que
respecto de un sistema y una estructura dados no hay ambigüedad
posible.
Segunda etapa: en lo que sigue
se tratará sólo de la conexión entre sistemas y estructuras si es posible establecer
una relación de simbolización tal como ha sido
señalada en la primera etapa. Podría ‘ocurrir entonces que lo afirmado por un
teorema de S rige en la estructura E. Por ejemplo, podríamos tener en S el teorema
“5
> 3" y podría ocurrir que en la estructura E 5 es mayor que 3 (o
sea, la relación biposicional
mayor rige entre
5 y 3). Hasta podría presentarse el caso de que lo afirmado por todos los teoremas de S rige
en la estructura E. Entonces decimos que la estructura E es un modelo de S o, a la inversa, que
S es un sistema
apropiado de E.
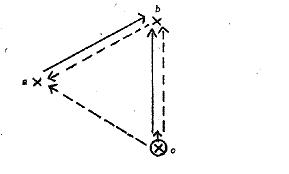
Una representación gráfica de
esta conexión sería:

Una estructura es científicamente
interesante sólo si el hombre de ciencia dispone de un sistema apropiado para
la estructura o esta empeñado en construir uno. Si tiene un sistema
apropiado entonces automáticamente lo que dice un teorema rige en la
estructura; conocer teoremas significa ser capaz de señalar conexiones entre
los elementos de la estructura.
Para demostrar concretamente que
un sistema es apropiado basta probar que lo afirmado por los axiomas rige en la
estructura. Con esto afirmado por los demás teoremas del
sistema también rige en la estructura, siempre que se trate de los sistemas aquí considerados, basados en el sistema funcional
básico. Así la demostración de que un sistema es apropiado es más fácil
que lo que aparece a primera vista.
Lo afirmado por algunos teoremas
rige en todas las estructuras. Son aquellos teoremas que pertenecen al fondo
lógico común, o sea, al sistema funcional básico. Por
lo tanto este sistema es apropiado para todas las estructuras o, a la inversa,
todas las estructuras son modelos del sistema funcional básico.
Ejercicio 4.1). Para
ilustrar la relación de simbolización se
podrían pegar objetos pequeños en una hoja de papel y escribir una o más letras
minúsculas latinas al lado de cada uno, pero de tal modo que ninguna letra este
al lado de dos o más objetos. Desgraciadamente este procedimiento no es
aplicable a todos los individuos, sea por su tamaño (elefante), su carácter
abstracto (el número 7), etc. Menos aún es aplicable a las
funciones proposicionales. Así, en general, conviene proceder en
forma abstracta, ejemplo: la cifra 0 simboliza el número 0, la cifra ‘1’ simboliza el numero 1, .
. ., la expresión “Par” simboliza la clase de los números pares, el signo "<"
simboliza la relación menor, etc.
Hacer una lista de símbolos individuales y funcionales e
indicar (en palabras) lo que símbolizan.
Ejercicio 4.2) Indicar en castellano algunos
teoremas generales tales que lo afirmado por ellos rige en todas las
estructuras. Ejemplos: “Algún individuo pertenece a F o no es el caso que algún individuo,
pertenece a F, “Si
todos los individuos que pertenecen a la subclase F pertenecen también a G y todos los que pertenecen a G pertenecen a H, entonces todos los que pertenecen a F pertenecen a H».
Ejercicio 4.3) Indicar en castellano algunos
teoremas específicos tales que lo afirmado por ellos rige en una de las
estructuras indicadas en los ejercicios de la
sección 2. Ejemplos posibles: "Todas las estaciones destinadas al
transporte de personas están modernizadas", "Algunas estaciones no
son vecinas de todas las estaciones", "Algún elefante no está en relación
Ed con algún elefante".
Se
puede demostrar que, dada una estructura, existen siempre infinitos sistemas
apropiados para ella. Es tarea del científico, especialmente del matemático,
encontrar uno y ojalá uno que proporcione mucha información, porque (según la
definición un indicada) hay sistemas apropiados constituidos únicamente por teoremas que no
proporcionan información específica sobre la estructura (ejemplo, el sistema
funcional básico). Lo ideal sería un sistema apropiado
que proporcione el máximo
de información, o sea que, para cada conexión,
simple o compleja, que rige en la estructura, haya un teorema del sistema que
la exprese. Hay una definición formal de "sistema que
proporciona
el máximo de información"; el sistema que lo
hace se llama "sistema completo respecto de la validez".
Para ciertas estructuras hay
sistemas completos, para otras hay sistemas apropiados mas y más informativos,
pero no hay uno que proporcione el máximo de información, porque se puede demostrar
que siempre hay otros con más información todavía.
Así como para cada estructura hay infinitos
sistemas apropiados, también a la inversa, para cada sistema
del tipo aquí considerado que está libre
de contradicción hay infinitas estructuras que son sus modelos.
Puede suceder que muchas de
estas estructuras tengan cierto parecido especial entre si, parecido que en
matemática se llama "isomorfía". Para aclarar un
poco este parecido consideremos dos estructuras E y E’,
más explícitamente:
<V,F,G>
<V',F',G'>
Supongamos que se puede
establecer una correspondencia biunívoca entre V y V', o sea que a cada
elemento de V puede asignarse
exactamente uno de V' y viceversa.
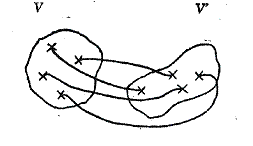
Si a, b, c, etc., son
elementos de V, entonces simbolizamos por "a' ", "b' ’, "c' ",
etc., los elementos correspondientes de V'. Supongamos que siempre cuando F rige entre a y b entonces
F' rige entre a' y b’ y algo análogo
respecto de G y G' y lo mismo para todos los elementos
de V en general
y sus correspondientes de V'.
En este caso decimos que E y E’ son isomorfos.
Utilizando palabras simples,
diremos que isomorfía significa que se puede establecer una correspondencia
biunívoca entre las clases V de tal modo
que los elementos correspondientes satisfagan siempre las funciones proposicionales
correspondientes.
La isomorfía es fundamental para
la matemática actual y en general para el tratamiento estructural. Al analizar
un campo se determina una de sus estructuras y se aprovechan luego los
resultados obtenidos respecto a esta estructura no sólo en el campo mismo
sino además en todos aquellos campos, tal vez muy lejanos, donde hay
estructuras isomorfas con la primera. Para usar la isomorfia no
importa cuáles son los elementos de V,
ni cuáles las funciones proposicionales; lo único que importa es que estén
relacionados de la misma manera.
Según la definición indicada cada estructura
es isomorfa consigo misma, y si E es isomorfa con E' también E' es isomorfa con E. Además, si E es isomorfa con E' y E’ con E”, entonces E es isomorfa
con E”. Si E es modelo del sistema S y
E' es isomorfa con E, entonces E' también es modelo de S (se
cambia correspondientemente la relación de simbolización;
por ejemplo, lo que antes era símbolo de F es ahora símbolo de F').
A veces no se hace distinción
entre estructuras isomorfas, y se tratan como si fueran una sola estructura;
pero según la terminología de este trabajo, E
y E', aunque isomorfas,
son diferentes, a menos que la clase V y las funciones proposicionales de E sean idénticas a las de E'.
Ejercicio 5.1) Indicar una secuencia S, S’, S”,
etc., de sistemas apropiados de una estructura,
donde S’ es más informativo que S, S'' más informativo que S’, etc. Ejemplo
respecto a la estructura <el, Mas1,
Ed2,
Pes2> del ejercicio 2.2: S es la clase de los teoremas del sistema funcional
básico con Mas1, Ed2
y Pes 2; S’ tiene además “Algún elefante
es masculino” y todo lo que se puede deducir a partir de este axioma; S''
tiene, aparte de los teoremas de S y S’, el axioma “Algún elefante
no es masculino” y todo lo que se puede deducir de esta expresión, etc.
Ejercicio 5.2) Indicar
una estructura donde los individuos son los personajes principales de un drama
o cuento; como mínimo conviene que la estructura tenga una función uniposicional
y dos biposicionales. Ejemplo:
<ham, Veng1, Mat2, Res2>, donde
ham es la clase de los personajes
principales de HAMLET, o sea, Hamlet (h), el rey Claudio (c), la reina Gertrudis (g), Polonio (p), Laertes (l) y Ofelia (o); Veng es la clase de
los que planean una venganza, Mat es
la relación de matar (físicamente) y Res es
la relación de ser indirectamente responsable de la muerte. La representación
gráfica sería:
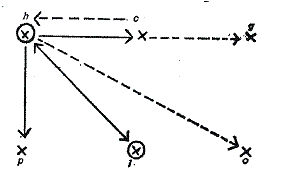
Los círculos marcan
aquellos que planean una venganza.
Ejercicio 5.3) Describir una situación que constituya una estructura isomorfa a la del ejercicio 5.2,
pero de un campo muy alejado. Hay
que demostrar punto por punto que las dos estructuras son isomorfas. Ejemplo: En una pieza hay
dos lámparas, encendidas (h' y l') que se iluminan mutuamente. Además, la
primera lampara (h’) ilumina una silla (p') y una mesa (c'). Sobre
la mesa está puesta la lampara h' y en uno de sus cajones el libro (g'). En el tubo de la lámpara
está puesto un resorte (o') que permite subir y bajar la
lampara. Tenemos así la estructura <pi,
Lam1, Il2, Pu2>, donde los individuos
son los objetos de la pieza, es decir, h',
c', g', p', l', o';
Lam es la clase de las
lámparas, Il la relación ilumina a y Pu la relación tener
puesto encima o adentro. Utilizando las letras del
ejercicio 5.2 con primas (“h' ”, etc.) se ve que hay una
correspondencia biunívoca entre ham y pi (h ‑h', c ‑ c', etc.).
Mientras que h y l pertenecían a la clase Lamp. Donde había la relación Mat ("®")
hay ahora la relación Il y
donde había la relación Res (“‑ ‑
‑‑>”)
hay ahora la relación
Pu. Tenemos la misma representación gráfica que en el
ejercicio 5. 2, sólo hay que cambiar las letras simples (“h”, etc.)
por las letras correspondientes con primas (“h' ”, etc.).
6. Clases de estructuras
En la sección 5 vimos que para cada sistema libre
de contradicción hay infinitas
estructuras que son sus modelos. Muchas de estas estructuras pueden ser isomorfas entre si, pero los sistemas
habituales
tienen también siempre, como modelos, estructuras no isomorfas entre si.
La clasificación más usada de
las estructuras se efectúa justamente por hacer
referencia a los sistemas de que son modelos. Concretamente, a una clase pertenecen todas las estructuras que son modelos del
sistema S1, a otra, todas las estructuras que son modelos de S2,
y así sucesivamente.
Por de pronto, la clasificación mencionada da
clases mucho más amplias que una clasificación por isomorfismo. Pero ella no es
exclusiva. Por ejemplo, una estructura E puede ser modelo tanto del sistema S1 como
también del sistema S2 y tal vez también de
S3 y de otros (vimos que toda estructura es modelo del sistema
funcional básico). A pesar de la falta de exclusividad, se prefiere en el
tratamiento estructural dentro y fuera de la matemática la clasificación
respecto de sistemas a toda otra clasificación posible.
Así, en
matemática tenemos la clase de las estructuras que son modelos de sistemas
como el de los grupos, el de los anillos, el de las álgebras de Boole[2] y otros. Aquellas estructuras que son
modelos del sistema de los grupos (que pertenecen a la clase correspondiente
de estructuras) se llaman simplemente “grupos”; las que
son modelos del sistema de los anillos se llaman «anillos»; las que son modelos
del sistema de las álgebras de Boole se llaman "algebras de Boole”, etc. Tenemos de este modo
una larga lista de estructuras matemáticas
con nombres especiales[3] y nada nos impide extender este tipo de
clasificación a otros campos.
Para dar un ejemplo matemático, sea V la clase de los números enteros, F la función proposicional biposicional de igualdad y G la función proposicional triposicional de
suma; luego <V, F, G> es (entre
otras cosas) un grupo, porque para esta estructura rige lo afirmado por los
axiomas (y demás teoremas) del sistema de los grupos. Hay infinitos otros
grupos, algunos de ellos isomorfos con <V,
F, G>, otros
no.
7. Estructura y realidad
Hasta el momento se correlacionó algo
no lingüístico,
que son las estructuras, con algo lingüístico, que son
los sistemas. Hay una sola excepción; son aquellas estructuras en que la clase
V a su vez está constituida entera o
parcialmente por expresiones, de modo que ya la estructura
misma tiene algo de lingüístico. En este caso se atribuye un carácter especial a los sistemas apropiados; se dice,
en terminología logicomatemática, que están formulados en "Ienguaje de segundo nivel",
o en "metalenguaje”, de modo que las
estructuras (parcialmente) lingüísticas estarían correlacionadas
con sistemas metalingüísticos.
Volviendo a aquellas estructuras que son
entes no lingüísticos (y de las cuales las recién señaladas no se distinguen
fundamentalmente), uno puede preguntarse si, o hasta qué punto, constituyen la
realidad. ¿Son, por lo menos en parte, el mundo objetivo?
La respuesta es más bien negativa, pero toda
la problemática es muy compleja. Por de pronto hay que ver las estructuras como
construcciones mentales elaboradas por hombres de ciencia, como productos de
la actividad racionalizadora humana, que tal vez
reflejen mas o menos fielmente ciertos aspectos de la realidad. Más no se puede
pretender. No se sabe siquiera si la realidad tiene un carácter estructural.
Además hay diferentes estructuras que corresponden a un sistema o a sistemas
igualmente bien apoyados en la experiencia. Es posible que en estos casos la
realidad excluya todas las estructuras, excepto una. Sin
embargo, también es posible que varias estructuras reflejen igualmente bien
ciertos aspectos de la realidad; pues hay que tener en cuenta que todo trabajo
científico constituye una simplificación
y que en esta simplificación una estructura puede reflejar, hasta
cierto punto, los aspectos A y otra los aspectos B de la realidad.
Aunque no podemos
afirmar que una estructura sea la realidad o parte de la realidad o una
copia fiel de la realidad, no por eso las estructuras están totalmente desvinculadas
de la realidad. Si los sistemas apropiados correspondientes están
apoyados ,directa o indirectamente en la experiencia, entonces las
estructuras modelan o simulan la experiencia ya obtenida y posiblemente futuras
experiencias, por lo menos con cierta aproximación.
De este modo la razón y la experiencia juntas nos guían en la preselección de
estructuras, nos ayudan en su construcción por etapas y nos hacen descartar
algunas estructuras a favor de otras.
Pero todo esto no constituye una
justificación suficiente para hablar de estructuras naturales (independientes
de los hombres teoretizantes) que se encuentran en las cosas.’ Por otro lado,
la pregunta por la existencia de una tendencia mental especial de formar
estructuras o de preferir ciertas estructuras a otras, pertenece al campo de
la psicología y no se tratará aquí.
Ejercicio 7.1) Indicar una estructura puramente lingüística donde ex es una clase determinada de expresiones
y se consideran relaciones como ser expresión
más larga
(con más signos) y ser sinónimo..
Ejercicio 7.2) Señalar (en metalenguaje)
algunos teoremas de la estructura del ejercicio 7. 1
8. Análisis
estructural de objetos y entidades simples
Es de interés aplicar las
consideraciones estructurales no sólo a campos más o menos extendidos del saber, sino también a objetos que se
presentan como algo simple a los sentidos, tales como una piedra, una manzana,
una melodía o a entidades no muy complejas, como una familia.
En algunos casos especialmente simples, hasta
un análisis conjuntivista es suficiente, mientras
que en otros un análisis estructural es más provechoso. Por ejemplo, para una
colección dada de estampillas puede ser suficiente considerar cuáles son las estampillas
que pertenecen a la colección y cuáles no. Tal vez no
interesa el orden en que las estampillas están pegadas en el álbum, ni cuál
estampilla es una variante de otra, cuál es más valiosa que otra, etcétera. En
este caso basta un análisis conjuntivista; la ‘colección se trata
simplemente como la clase o el conjunto de las estampillas. Si, en cambio, se
desea tener en cuenta las relaciones arriba mencionadas u otras similares
habría que considerar una estructura como <est, Ant, Var,
. . . >, donde est (o sea V) sería la clase de las estampillas, Ant la relación
biposicional figurar con anterioridad
en el álbum, Var la relación biposicional
ser una variante de, etc.
En muchos otros casos el análisis
conjuntívista es de antemano insuficiente; no hasta tratar una pared
como una clase de ladrillos, una piedra como una clase de moléculas, una
manzana como una clase de células o de moléculas, una melodía como una clase de
sonidos. En todos estos casos debe considerarse un determinado número de
funciones proposicionales, aparte de la clase que se elige para formar la base
de la estructura respectiva.
Así tendríamos para una pared
determinada hecha sólo de ladrillos, sin argamasa, algo como <lad,
Tar,
Tis, . . . >,
donde lad seria la clase
respectiva de los ladrillos, Tar la
relación biposicional topar en el plano por arriba, Tis, topar en el plano por la izquierda, también
con relaciones como topar en una línea,
topar en un punto y tal vez otras mas. Aplicando el mismo tratamiento a
todo lo que, en principio, uno está dispuesto a considerar como pared de
ladrillos, se pueden formar en general las estructuras correspondientes. No es
difícil
construir un sistema llamado tal vez “teoría de las paredes de ladrillos” que señala, mediante axiomas y teoremas
demostrados, las características comunes de todas estas estructuras en un sentido
muy amplio (incluyendo, por ejemplo, las estructuras isomorfas
con ellas). Los modelos del sistema serían, luego, paredes de ladrillos
(tratadas como estructuras) y estructuras isomorfas con paredes de ladrillos, todo en plena
analogía con los grupos, anillos y áIgebras de Boole.
Consideraciones similares, aunque más complejas,
se aplican a piedras, manzanas, etc., se construyen sistemas correspondientes y
se consideran luego los modelos de estos sistemas.
Una determinada melodía ejecutada (es decir,
interpretada
tal día y a tal hora) podría tratarse, en un análisis
muy primitivo, como <son, Ant, . . . >,
donde son seria la clase de los
sonidos respectivos (que a su vez son complejos e incluyen también la falta de
sonido, o sea, el silencio), Ant, la
relación de anterioridad y algunas relaciones más, según el
grado en que uno quiere profundizar el análisis. Un musicólogo probablemente
procedería en forma diferente; por un lado, no partiría de son sino de una clase de sonidos en
algún sentido básicos; por otro, no analizaría melodías ejecutadas sino melodías de tipo general que son
comunes a una variedad de ejecuciones. Estos detalles, aunque en sí muy
interesantes, no son esenciales para un tratamiento
general de las estructuras. En cualquier caso se procede, luego, a la
construcción de los sistemas correspondientes, lo que permite, posteriormente,
analizar los modelos de estos sistemas.
También una familia o un
regimiento son más que una clase de personas, al igual que un bosque es más que
una clase de árboles. Para una familia determinada en sentido biológico (sin
considerar aspectos legales) tenemos algo como <pers, Mas, Pam,
Cop, Cos,
. . . >, donde pers es la clase de los
integrantes de la familia, Mas la
función uniposicional ser de sexo masculino, Pam la relación biposicíonal ser padre o madre de, Cop
la relación biposicional
ser primer cónyuge (en orden
temporal) de, Cos
la relacion biposicional ser segundo cónyuge de. Análogamente un regimiento determinado puede
tratarse tal vez como <pers, Sa, Ten, . . . >,
donde, pers es la clase de los integrantes del
regimiento, Sa, la relación biposicional
ser sargento de,
Ten, la relación biposicional ser teniente de. Sin dificultad se
forman los sistemas correspondientes que tienen por
modelos familias (regimientos) y estructuras isomorfas con
familias (regimientos),
En el caso de los bosques un tratamiento simplificado
sería limitarse a los árboles y a las relaciones entre ellos.
Naturalmente nada nos impide profundizar el análisis incluyendo
en la clase V las demás plantas del
bosque, los animales y otros objetos que, según la opinión del que realiza el
análisis, tienen importancia. Una vez tomadas las decisiones previas respecto
de V y las funciones proposicionales,
se forman las estructuras y el sistema correspondiente.
Lo que se señaló aquí para objetos y
entidades simples (muy simplificadas en estas paginas) puede
extenderse también a casos mas complejos, como
estados psíquicos, lenguajes, economías
y sociedades. Pero entonces el grado de dificultad aumenta
enormemente, a menos que uno se limite a tomar en cuenta sólo unas pocas funciones
proposicionales.
9. Parte y entero
La relación parte ‑ entero es un problema interesante de la lógica. Ha
sido analizada a fondo en algunos casos especiales como el de subclase ‑ clase y de subestruetura
‑ estructura. En
cambio la relación entre lo que aquí se llamará «estructura parcial”
y la estructura entera no ha sido tratada en forma especial, que yo sepa
(véase, por ejemplo, [8] y [4] en la bibliografía).
Tengamos un triple <V, F, G> que es un grupo, o sea una estructura que cumple
con las condiciones señaladas en los, axiomas de la teoría de los grupos.
Formemos, además, un triple <V’, F’, G'>, donde V' es una subclase (no vacía) de V y F'
y G' con restricciones de F y G a V' (son F y G aplicadas
sólo a los elementos de V). Supongamos que <V’, F’, G'> también sea un grupo. En
este caso decimos que <V’, F', G'> es
un subgrupo
de < V, F, G>. Por
ejemplo, los números enteros (positivos, 0 y negativos) forman,
respecto de la igualdad y la suma, un grupo <ent, Ig, Su>. Lo mismo
hacen los números pares (positivos, 0 y negativos) respecto de igualdad y suma
restringidas a los números pares. Así <par, Ig’, Su'> es un subgrupo de <ent,
Ig, Su>.
Exactamente las mismas consideraciones pueden
aplicarse a cualquier estructura, de modo que podemos hablar de subparedes
de ladrillos, de subpiedras, submanzanas, submelodías, etc.
Se exige que V' sea una subclase de V,
en otras, palabras, que todos los elementos de V' sean elementos de V. Puede ser que también todos los elementos
de V sean elementos de V' (en este caso se dice que V’ es subclase
impropia de V) o que en V haya
elementos que no figuran en V’ (en
este caso se dice que V' es
suclase propia de V). Aplicando la definición de “subestructura” a
las subclases impropias, se ve que cada grupo
es subgrupo
de si mismo, cada piedra subpiedra de si misma.
Sin embargo, estos casos triviales en que V' es una subclase impropia
de V interesan menos que los casos en
que V' es una subclase propia de V (así, en el ejemplo, par es
subclase propia de ent).
Muchos grupos tienen subgrupos propios,
como es fácil de ver. Dada una pared de ladrillos de cierta extensión, se puede
encontrar una subpared propia, o sea, una subclase propia
de lad cuyos elementos cumplen,
respecto de las relaciones Tar‘, Tis’, etc., con las condiciones características de las paredes de
ladrillos. Algo análogo vale también para las piedras de cierto tamaño. En
cambio, la única submanzana de una manzana dada
es esta manzana misma, porque no hay una subclase propia de las células de modo que los elementos de esta subclase cumplan,
respecto de las funciones proposicionales correspondientes, con las
condiciones características de las manzanas (por lo menos en el caso ideal de
las manzanas a las que no les faltan partes).
Para melodías no demasiado cortas hay submelodías
propias, y lo mismo vale para familias más o menos numerosas. También hay subregimientos propios
(por ejemplo un regimiento después de los combates en relación con el
regimiento antes de los combates) e, igualmente, hay subbosques
propios.
Tenemos, así, un
tipo de relación parte ‑ entero que
ha sido ampliamente investigado, por lo menos en el caso de las álgebras
tradicionales, como grupos, anillos y álgebras de Boole. Se vio que la
extensión de este tratamiento a paredes, piedras y otros objetos no ofrece dificultades
en principio.
Sin embargo, hay casos en que la relación parte-entero no está comprendida en el
tratamiento de subestructuras. Así un cuarto de
manzana no es una manzana, una tajada de pan no es un pan. En todos estos casos
no se trata de subestructuras, porque las células
del cuarto de manzana o las moléculas de la tajada de pan no cumplen, respecto
de las funciones proposicionales correspondientes, con las condiciones
características de las manzanas o de los panes, respectivamente.
Por otro lado, las células del cuarto de manzana cumplen con algunas condiciones características de
las manzanas. En otras palabras, aunque <cel', F', G', . . .
> no es una submanzana de <cel, F, G, . . . >, los
elementos de cel’ cumplen, respecto de F', G',
etc., por lo menos con algunas de las condiciones señaladas en los
axiomas y demás teoremas del sistema que podría llamarse «teoría de las manzanas”. Habría que indicar cuáles son las condiciones
que se desean conservar y, eventualmente, cuáles son las condiciones
adicionales cuyo cumplimiento se exigirá
para las partes de manzanas.
Una vez hecho esto, se construye sin dificultad un sistema tal vez
llamado «teoría de las partes de manzanas”. Uno de
sus modelos sería entonces <cel', F', G',
. . . >; si, además, cel' es una subclase de cel y si F', G',
etc., son restricciones de F, G,
respecto de aquellas condiciones que se conservan, entonces <cel',
F', G', . . . >
podría considerarse como parte de <cel, F, G, . . . >.
La relación parte de manzana ‑ manzana seria entonces un nuevo tipo de
relación parte ‑ entero. Exactamente
el mismo tratamiento puede aplicarse a la relación tajada de pan ‑pan y a muchos otros casos. El nuevo
tipo de partes podría llamarse “estructuras parciales” (respecto de las
estructuras originales).
Hay muchas diferencias entre las
subestructuras,
por un lado, y las estructuras parciales, por otro. Así, para cualquier
estructura queda establecido en principio cuáles son sus subestructuras
(estructura y subestructuras respectivas son de la
misma clase). En cambio, en cada caso hay que fijar de nuevo
cuáles son las estructuras parciales de una clase dada de estructuras; por
ejemplo, se debe fijar qué es una estructura parcial respecto de las manzanas,
qué es una estructura parcial respecto de los panes, etcétera.
Vimos antes que cada estructura es subestructura
de si misma. En cambio una estructura no es necesariamente estructura parcial
de si misma (no lo es si para las estructuras parciales respectivas se fijan
condiciones adicionales que no se cumplen en las estructuras originales).
Una pregunta interesante se refiere a la
parte de la parte. ¿Es a su vez parte del entero? Respecto de las subestructuras
tenemos (según ‑la definición de «subestructura») el
resultado de que una subestructura de una subestructura de
una estructura es también directamente subestrura de la
estructura.
Tampoco aquí tenemos lo mismo para las estructuras
parciales. Supongamos que una miga de pan sea estructura parcial de una tajada
de pan (cumple con las condiciones características de las partes de tajadas de pan y hay la relación de subclase
entre las V respectivas y de
restricción entre las funciones proposicionales). Supongamos, además,
que la tajada a su vez sea estructura parcial de un pan entero (cumple con las
condiciones características de las partes de panes y hay la relación de subclase y de restricción). No por eso la miga es
necesariamente estructura parcial del pan entero, ya que no cumple
automáticamente con las condiciones características de las partes de panes. Depende del sistema de las partes de panes
elegido si, además de las tajadas, también las migas se consideran partes de
panes. Aunque así, en resumen, E1 (la miga) es estructura parcial de
E2 (de la tajada) y E2 es estructura parcial de E3
(del pan entero), no por eso E1 es automáticamente estructura
parcial de E3.
Los análisis recién señalados
nos proporcionaron algunos datos básicos sobre dos relaciones bien diferenciadas,
la de subestructura y la de estructura parcial. Ambas pueden tratarse
rigurosamente y son, hasta cierto punto, representativas de la relación
informal parte ‑ entero.
Ejercicio 9.1) Hacer una lista de ejemplos entero
‑ parte, subrayando aquellas expresiones de partes que simbolizan
subestructuras.
Ejercicio 9.2) Indicar teoremas que rigen para
una estructura y no para una de sus estructuras parciales y viceversa
(señalando previamente la estructura parcial). Ejemplo respecto a manzanas y
partes de manzanas (con Pul1, ser
célula de la pulpa y Ex1, ser célula que está en contacto con el exterior):
“Ninguna célula de
Pul es Ex".
10. El tiempo en el tratamiento estructural
Se señaló en la introducción que este trabajo, aunque dedicado a las estructuras, no
está dentro de la línea estructuralista, Así, el estructuralismo
generalmente trata las estructuras haciendo abstracción del tiempo, o bien las
enfoca en un determinado punto temporal, sin tener en cuenta, de este modo, los
cambios temporales, o sea, el desarrollo. En cambio, desde el punto de vista logicomatemático
no hay razón alguna para excluir los factores temporales, si estos son de
interés para el campo respectivo. Tampoco existen dificultades en principio
que impidan un tratamiento temporal.
Como ejemplo sencillo se señalará el caso de
las familias. Vimos que sin consideraciones temporales una familia puede
presentarse como k‑tuplo de la forma <pers,
Mas, Pam, Cop, Cos,
. . . >. En esta
estructura queda establecido quién es tío de quién, al igual que en un árbol genealógico;
pero no se toma en cuenta que el tío y el
sobrino hayan o no hayan vivido como contemporáneos durante un tiempo, ni quién
de. los dos haya nacido o muerto
antes. i
Para tratar ahora ciertos aspectos
temporales, consideremos una familia durante un
tiempo determinado, supongamos un siglo. Efectuamos un corte
temporal siempre que un integrante de la familia haya nacido, se haya casado,
haya muerto y tal vez haya intervenido en otros ‑acontecimientos que se
consideren importantes. Supongamos que el numero total de los cortes temporales
sea 80, aparte de las fechas claves que son el principio y el fin del siglo. El
siglo se descompone entonces en 81 trechos temporales.
Supongamos que el nacimiento de Jonás haya marcado el principio del trecho 17 y su muerte
el fin del trecho 60 (el principio del trecho 61). En vez de considerar a Jonás como un único elemento
de pers,
trataremos ahora a Jonás17, a Jonás18, ... a Jonás60
como elementos de una clase
pert, o sea, de una clase
cuyos elementos se llamarán "personas temporales". Se
procede de un modo análogo con los demás integrantes de la familia. Así pert tiene muchos más elementos
que pers
(en vez de un solo Jonás tiene 44 Jonás).
Ahora, pert nos servirá de
clase básica para una estructura en que aparte de Mas *, Fam *,
Cop *, Cos
* (las funciones proposicionales de la estructura
original atemporal modificadas correspondientemente para referirse ahora a los
elementos de pert), figuran numerosas
funciones proposicionales como presentarse
en el mismo trecho temporal que (por ejemplo, Jonás22 y
Pablo22), estar conectado evolutivamente con
(por ejemplo, Jonás22 con Jonás47),
etc.
Consideraciones análogas pueden aplicarse a
todas las estructuras, por ejemplo, a las piedras o, para mencionar un caso
donde el tiempo es de importancia, a los núcleos de átomos durante un lapso
determinado, usando en este caso como clase básica las partículas y
resonancias temporalmente limitadas (en analogía a Jonás17, etc.).
La lógica y la matemática tienen muchas otras maneras de considerar el tiempo, por ejemplo, incluyendo entre los individuos de la clase V los puntos temporales.
Todo esto nos permite ver que tiempo,
desarrollo e historia son perfectamente compatibles con el tratamiento estructural.
Ejercicio 10.1) Supongamos que tenemos los siguientes
individuos de pert: Carlos1,
Carlos2, Julia2, Carlos3, Julia3,
Carlos4, Julia4, Sonia4,
Julia5, Sonia5,
Sonia6. Supongamos, además, que sabemos que
sólo nacimiento, casamiento y muerte de una de las tres personas inician o
terminan un corte temporal. Escribir la historia de la familia. Ella comenzaría
así: Nace Carlos (el primer trecho corresponde a la vida de Carlos antes de
que Julia haya nacido), nace Julia... .
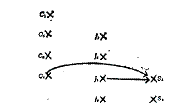
Ejercicio 10.2) Una
representación gráfica de los individuos del ejercicio 10. 1 con la relación Ser actualmente padre o madre de seria:
Representar (con otros tipos de flechas) las
relaciones presentarse en el mismo trecho temporal y estar conectado evolutivamente.
Ejercicio 10.3) Tengamos un pión negativo (p‑), este se desintegra
en un muón negativo (m‑) y un neutrino (n), luego el muón se
desintegra en un electrón (e‑), otro neutrino (n') y
un antineutrino (`u). a)
Indicar la clase part de las partículas
temporales. b) Representar gráficamente la estructura
<part, Noc1, Des2,
Ev2>, donde
Noc es la clase de aquellas partículas
(temporales) que no tienen carga eléctrica (es decir, las partículas temporales que corresponden
a los dos neutrinos y al antineutrino), Des
es la relación ser producto directo de la desintegración de
y Ev la relación estar conectado
evolutivamente
(entre partículas
temporales que corresponden a una misma particula).
11. Conclusión
Si prescindimos de consideraciones
especulativas y nos limitamos a un tratamiento estructural del tipo aquí indicado,
vemos que éste constituye un método muy fructífero. En el estado actual de las
ciencias tiene aplicación universal, o sea, el tratamiento estructural puede
imponerse, con más o menos ventaja, a todo campo teórico
(se construye la clase V, se establecen las funciones
proposicionales que son de interés, luego se forma el k‑tuplo, etc.) Sin
embargo, no se debe sobrevalorar este
tratamiento en forma unilateral ni olvidar que hay otros métodos que pueden ser
igualmente fructíferos.
1. Carnap, R.: The
Logical Structure of the World ‑ Pseudo‑problems in
Philosophy. Berkeley, Los Angeles, 1969.
2. Piaget,
J.: Le structuralisme. Paris, 1968.
3. Pingaud,
B. y otros: Lévi‑Straws:
Estructuralismo y dialéctica. Buenos Aires, 1968.
4. Rescher,
N.: Axioms for the Part Relation, Philosophical
Studies, vol. 6. Minneapolis, 1955, págs. 8‑11.
5. Robinson,
A.: Introduction to Model Theory
and the Metamathematics of Algebra. Amsterdam, 1963.
6. Stahl,
G.: Elementos
de metamatemdtica, Santiago, 1973.
7. -----:
“Linguistic Structures Isomorphic to Object Structures”. Philosophy and Phenomenological
Research, vol. XXIV, nº 3, 1964, pAgs. 339‑344.
8. ------‑
“Termes temporals dans des systèmes fonctionnels”, Revue Philosophique de
9. Tarski,
A. Foundations of the Geometry of
Solids, en Logic, Semantics, Metamathematics, Oxford, 1956, págs.
24‑29.