
Teoría de conjuntos
Pulsar aquí para revisar el listado de SÍMBOLOS
1. CONJUNTOS Y ELEMENTOS
En lo que sigue utilizaremos a menudo conceptos de la Teoría de Conjuntos. Además de sus conexiones con la lógica, la teoría de conjuntos es fundamental en matemáticas y tiene una serie de aplicaciones en lingüística. Por todo ello, vamos a comenzar por una breve caracterización de los conceptos más importantes en este campo.
Un conjunto, es una agrupación o colección de cosas o entidades de cualquier tipo. Otros términos que se utilizan a menudo para referirse a conjuntos son los de 'clase' y 'grupo' (aunque estos términos tienen otros usos técnicos diferentes en matemáticas). Un conjunto consiste en una serie de elementos o miembros. En la vida cotidiana hablamos habitualmente de conjuntos de elementos que tiene algo en común, por ejemplo hablamos de todos los suecos o del conjunto de los libros en una cierta biblioteca. La teoría de conjuntos no establece tal restricción sobre la formación de conjuntos: un conjunto puede formarse a partir de elementos entre los cuales no existe ninguna relación. Podemos por ejemplo decidir formar el conjunto consistente en el Primer Ministro sueco, el más pequeño de los satélites de Marte y la raíz cuadrada de 7.
Algunas convenciones sobre la notación: usaremos letras latinas mayúsculas (A, B, C...) para referirnos a conjuntos y letras latinas minúsculas (a, b, c...) para referirnos a los objetos singulares que son elementos de los conjuntos. Introducimos un símbolo especial, Î, que se lee 'es un elemento de' o bien 'es un miembro de.' Por ejemplo, 'a es un miembro de B' se escribe a e B. Si queremos decir que a no es un miembro de B, escribimos a ÏB.
Necesitamos también una notación para escribir expresiones tales como 'el conjunto formado por las siguientes personas: ‘Juan, Guillermo, Enrique' o 'el conjunto de los españoles pelirrojos'. Para estos casos empleamos llaves, { }. Como se trasluce de los ejemplos empleados, hay al menos dos maneras de definir conjuntos: por enumeración y por descripción. Utilizando llaves nuestros ejemplos cobrarían el siguiente aspecto:
Enumeración: {Juan, Guillermo, Enrique}
Descripción: {x/x es español pelirrojo} (léase: 'el conjunto de los x tales que x es español pelirrojo)
Existen también expresiones del lenguaje cotidiano para expresar esto. Las enumeraciones se forman habitualmente con la conjunción y por ejemplo: Juan (y) Guillermo y Enrique, y para las descripciones utilizamos oraciones de relativo, p. ej.: los que son españoles.
Aunque puede resultar extraño, la teoría de conjuntos permite conjuntos cuyo número de elementos es uno o cero. Para cada individuo u objeto en el mundo, hay un conjunto que tiene como único elemento ese individuo u objeto. Por ejemplo, dada una persona a, podemos formar el conjunto {a}. Es importante recordar que a y {a} son cosas diferentes: a no es un conjunto.
Un conjunto con un único elemento se llama conjunto unidad. Un conjunto que no tiene elementos (que tiene cero elementos) se llama conjunto vacío, o mejor, el conjunto vacío puesto que sólo hay uno. Lo denotamos con el símbolo Æ La razón de que sólo exista un conjunto vacío estriba en un principio general de la teoría de conjuntos, el principio de extensionalidad, que afirma lo siguiente: dos conjuntos son diferentes entre sí exactamente cuando existe al menos una cosa que es elemento de uno y no del otro. En otras palabras, si la lista de elementos es la misma, estamos operando con el mismo conjunto. Todo conjunto vacío tiene, evidentemente, la misma lista de elementos, así que no hay más que un conjunto vacío. Una consecuencia ligeramente paradójica de todo esto es que, por ejemplo, el conjunto de todas las mujeres que han sido Presidente de los EE.UU. es idéntico con el conjunto de los perros que escriben programas de computadora. De todos modos entenderemos esto mejor si observamos la diferencia entre (a) el modo en que se escogen los elementos de un conjunto (los criterios para distinguir entre elementos y no‑elementos) y (b) los elementos que de hecho se han escogido. Es claro que los mismos elementos se pueden escoger de modos muy diferentes. La idea del principio de extensionalidad es prescindir, totalmente del modo en que los elementos de un conjunto han sido elegidos. Esta distinción está relacionada con otra que tendrá gran importancia en los capítulos siguientes: la distinción entre intensión y extensión de una expresión en un lenguaje: Estudiemos un sintagma nominal que, describe un conjunto, p. ej.: los españoles pelirrojos. Podemos decir que este sintagma selecciona (o se refiere a) ciertas entidades o cosas en el mundo por medio de una especificación de ciertas propiedades que les son comunes. Las entidades seleccionadas ‑esto es, las personas que son españolas y pelirrojas‑ constituyen la extensión del sintagma nominal, mientras que el modo o manera en que son seleccionadas ‑esta es, los criterios usados para determinar la extensión de la expresión‑ sería la intensión del sintagma. Vemos ahora que el concepto de 'conjunto' en la teoría de conjuntos se puede considerar extensional en el sentido de que no hay que preocuparse por el modo en que los miembros de un conjunto se seleccionan. De ahí el nombre de principio de extensionalidad.
Lo que llevamos dicho pone de manifiesto que el concepto matemático de conjunto no coincide exactamente con el concepto cotidiano al que nos referimos con palabras como 'clase' o 'grupo', aunque provisionalmente lo hayamos supuesto al principio de este capítulo. Cuando hablamos de grupos en la vida cotidiana, por ejemplo al hablar de grupos de personas, pensamos en ellos como sí fueran el mismo en momentos diferentes del tiempo, aunque sus miembros cambien. Así, por ejemplo, hablamos del grupo de personas que gobiernan Inglaterra, diciendo incluso cosas como este grupo tiene más miembros de los que solía tener, un enunciado que sería contradictorio si supusiéramos que el principio de extensionalidad es válido para la entidad que designamos con este grupo. Nótese también que hay muchas cosas que se pueden decir de los grupos, por ejemplo que realizan tal o cual acción (colectiva) ‑tal sería el caso en Nuestro grupo envió una petición al gobierno‑, mientras que por lo menos algunos matemáticos dirían que los conjuntos son entidades abstractas que no hacen tales cosas.
Otro conjunto especial es el conjunto universal, que simbolizamos con 1 (el número uno). Para explicar el conjunto universal, hemos de introducir una nueva noción, la de universo del discurso, que puede definirse sin pretensiones de exactitud, como 'todo aquello de lo que se habla en un cierto texto o conversación'. Por ejemplo, en un libro de matemáticas el universo del discurso pueden ser todos los números, mientras que en un manual de física podrían serlo todos los cuerpos físicos. El conjunto universal será, pues, el conjunto de todos los objetos en el universo de discurso pertinente.
2. RELACIONES ENTRE CONJUNTOS
Hay una serie de conceptos en la teoría de conjuntos que se refieren a las relaciones entre conjuntos. Estas relaciones se pueden representar dibujando los conjuntos como círculos. Consideremos por ejemplo el conjunto de todos los europeos y el conjunto de todos los ingleses. Dado que todos los ingleses son europeos podemos dibujar el diagrama (1) para representar las relaciones entre los dos conjuntos, siendo A el conjunto de los europeos y B el conjunto de los ingleses.

En tal caso, decimos que B es un subconjunto de A o que B está incluido en A. En teoría de conjuntos se distinguen normalmente dos relaciones: inclusión e inclusión propia. Decimos que un subconjun B es un subconjunto propio del conjunto A, cuando todos los miembros de B son miembros de A y además hay al menos un miembro de A no, es miembro de B. Escribimos A Ì B con el símbolo Ì para 'es subconjunto propio' o 'está incluido estrictamente en'. Si, como ocurre a menudo, no afirmamos que A contiene al menos un elemento que pertenece a B, escribimos B Í A, que quiere decir simplemente 'B e incluido en A' o 'B es un subconjunto de A'.
Si queremos decir que A y B son el mismo conjunto ‑en otras palabras, que son idénticos‑, escribimos A = B. Hemos visto en la sección precedente que esto significa que A y B tienen los mismos elementos.
Es importante distinguir entre las relaciones 'es un elemento, de' ('es un miembro de') y 'es un subconjunto de'. El conjunto de los ingleses es un subconjunto del conjunto de los europeos, pero no es un elemento de ese conjunto. John Smith, por otro lado, es un elemento del conjunto de los ingleses, pero no un subconjunto de ese conjunto.
3. OPERACIONES CON CONJUNTOS
Hay, conjuntos cuyos elementos son a su vez conjuntos. (Tales conjuntos se llaman a veces colecciones o familias). Por ejemplo, es posible formar, a partir de cualquier conjunto A el conjunto que contiene todos los subconjuntos de A. Este conjunto se llama conjunto potencia de A. Ejemplo: El conjunto {a, b} tiene los siguiente subconjuntos: {a}, {b}, {a, b}, Æ (El conjunto vacío es un subconjunto de cualquier conjunto.) El conjunto potencia de {a, b} es pues {{a}, {b}, {a, b}, {Æ}.
Para distinguir los conjuntos de conjuntos de los conjuntos ordinarios, nos referiremos a ellos utilizando mayúsculas: A.
Hemos hablado, de diferentes maneras de definir conjuntos. Un conjunto puede también definirse en términos de otros conjuntos por medio de las llamadas operaciones con conjuntos. Dados dos conjuntos A y B, podemos definir el conjunto formado Por los objetos que son elementos de A y de B. Llamamos a este conjunto intersección de A y B y lo simbolizamos con A Ç B. En (1) la intersección de A y B viene indicada por el área sombreada

Ejemplo: Si A es el conjunto de los lingüistas y B es el conjunto de los suecos A Ç B es el conjunto. de los lingüistas suecos.
Puede ocurrir también que queramos hablar del conjunto de los objetos que son elementos de al menos uno de los conjuntos A o B. Este conjunto se llama unión de A y B y se simboliza por A È B. Corresponde al área sombreada en (2).
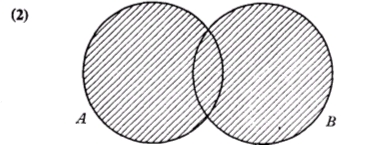
Ejemplo: Si A es el conjunto de las personas que han leído Guerra y Paz y B es el conjunto de las personas que han leído Ana Karenina, entonces A È B es el conjunto de la gente que ha leído Guerra y Paz o Ana Karenina (o ambos).
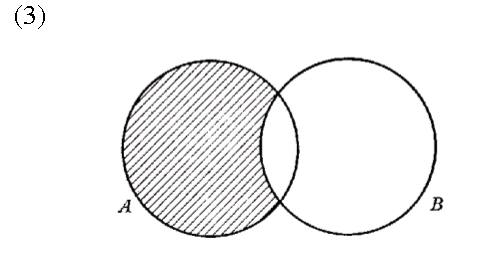
El conjunto sombreado en (3), esto es, el conjunto de elementos que son miembros de A pero no lo son de B, se llama diferencia de A y B y se simboliza A ¾ B (léase 'A menos B'). Ejemplo: Si A es el conjunto de los ingleses y B el conjunto de las personas que hablan portugués, A ¾ B es el conjunto de los ingleses que no hablan portugués (todos los ingleses excepto aquellos que hablan portugués).
Hasta ahora hemos hablado de operaciones con pares de conjuntos. No hay nada, sin embargo, que nos impida ampliar las operaciones de modo que se apliquen a tres o más conjuntos. Podemos, por ejemplo, definir la intersección de A, B, C, D (el conjunto formado por los elementos comunes a los cuatro conjuntos A, B, C y D) como una operación con el conjunto de conjuntos {A, B, C, D} que se puede simbolizar por medio de n {A, B, C, D} (el área sombreada en (4)).

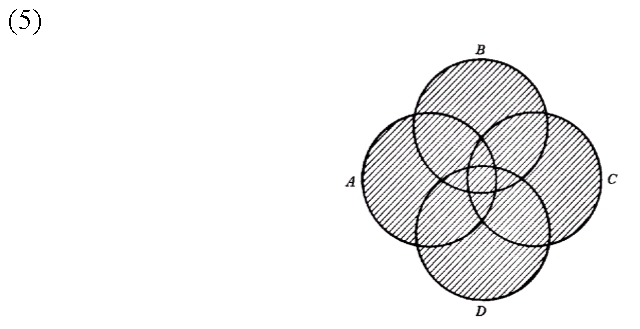
Del mismo modo, podemos simbolizar con È {A, B, C, D} la unión de A, B, C y D (el conjunto que contiene los objetos que son elementos de al menos uno de los conjuntos A, B, C y D). La unión de estos conjuntos corresponde en el diagrama (5) al área sombreada.
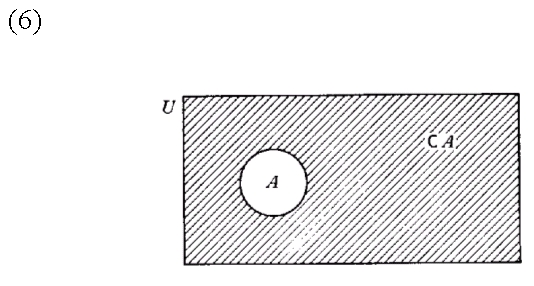
Otro concepto importante es el de complemento de un conjunto. Dado cierto universo de discurso U, por ejemplo el conjunto de todos los seres humanos, y un subconjunto A de este conjunto, por ejemplo, el conjunto de los franceses, podemos hablar del conjunto de los miembros de U que no son miembros de A, es decir, en este caso, del conjunto de los seres humanos que no son franceses. Este conjunto se llama complemento de A respecto a U. en (6) el rectángulo es U, el círculo es el conjunto A y el área sombreada es el complemento de A, que se simboliza con CA o con A-.
4. RELACIONES Y FUNCIONES
Un conjunto de dos elementos se llama par. Si decidimos considerar que los elementos del par están ordenados en alguna manera, obtenemos un par ordenado. Para simbolizar los pares ordenados utilizamos paréntesis en ángulo < > en vez de llaves { }. (A veces se utilizan paréntesis ordinarios ( ) ). Cuando manejamos pares no ordenados, el orden en que enumeramos los elementos no tiene importancia. Por ejemplo {a, b} es el mismo conjunto que {b, a}. El par ordenado <a, b>, sin embargo, no es necesariamente idéntico con el par ordenado <b, a>. Para dejar esto en claro, vamos a estudiar brevemente el concepto de relación, que discutiremos más detalladamente en la sección 5.8. Una relación diádica, por ejemplo, 'ser más inteligente que' se da entre dos objetos singulares, que han de ser considerados como miembros de un par ordenado. Es claro que el orden en que se dan los dos objetos es esencial: 'Hengist es más inteligente que Horsa' no es lo mismo que 'Horsa es más inteligente que Hengits'.
Del mismo modo podemos hablar de TRIO ordenado (con 3 elementos), CUÁDRUPLO (4 elementos), QUNTUPLO (5 elementos), y, en general, N‑TUPLO. (Corresponden a relaciones de 3, 4, 5 y n lugares o argumentos, respectivamente). Los días del año, por ejemplo, pueden considerarse un 365‑tuplo ordenado.
Un concepto, muy importante en lógica, matemática y lingüística es el de función. Veamos un ejemplo. Todo automóvil tiene una matrícula.
Consideremos ahora el conjunto de los automóviles y el de las matrículas. Lo, representamos en el diagrama (1):

Cada x representa un elemento en su respectivo conjunto (puede haber, desde luego, más elementos). De cada elemento en el conjunto, de la izquierda, es decir, el conjunto de los automóviles parte una flecha hacia un elemento en el conjunto de la derecha, a saber, hacia la matrícula correspondiente a cada coche. De esta manera obtendríamos un gigantesco número de pares ordenados en los que el primer elemento, es un coche y el segundo, su matrícula: así por ejemplo, <el coche de Paco Pérez, M‑27.552>. Hemos asignado a cada elemento en el primer conjunto un elemento del segundo conjunto. Tal asignación se llama función. Para que exista una auténtica función es necesario que haya exactamente un elemento en el segundo conjunto por cada elemento en el primer conjunto (es posible, sin embargo, que varios elementos en el primer conjunto compartan un solo elemento en el segundo conjunto). En otras palabras, las flechas pueden ser convergentes pero no divergentes. (Volveremos sobre este punto al estudiar las propiedades formales de las relaciones en la sección 5.8).
Supongamos ahora que tenemos dos conjuntos A y B como en la figura (2), y una función (simbolizada por la flecha) que asigna un elemento distinto de B a cada elemento de A. Decimos que tenemos una función inyectiva de A en B, o bien una función que PROYECTA A en B. Esta última expresión puede parecer extraña al principio, pero se usa a menudo en la bibliografía técnica lingüística. Por ejemplo, una transformación en una gramática transformacional puede ser considerada como una función que proyecta un conjunto de estructuras en otro conjunto de estructuras, lo cual es un modo imaginativo de decir que para cada estructura que 'entra' en la transformación hay exactamente una estructura que 'sale' de ella.

Otros ejemplos cotidianos de funciones se encuentran, por ejemplo, en cualquier libro que tenga tablas estadísticas. Por ejemplo, podemos encontrarnos con un listado de los países de Europa y su población (3): Un cuadro estadístico de este tipo representa una función en la que la columna de la izquierda corresponde al conjunto A en (2) y la columna de la derecha, al conjunto B. En otras palabras, tenemos una función que proyecta el conjunto de los países el conjunto de los números.
(3)
| Albania | 2,337,600 |
| Andorra | 25,000 |
| Austria | 7,456,403 |
Debemos explicar alguna terminología más. Cada elemento de la columna de la izquierda es un argumento de la función, y el correspondiente elemento de la columna de la derecha es el valor de la función para ese argumento. Denotamos la función misma como letras minúsculas a partir de la f, y escribimos f(x) para indicar el valor de la función f para el argumento x. Si f es la función representada en la tabla anterior, podemos, por ejemplo, escribir f (Suecia) = 8.000.000 para indicar que la función toma el valor 8.000.000 para el argumento Suecia; en otras palabras, que la población de Suecia es ocho millones.
El conjunto de los posibles argumentos de una función (por ejemplo, el conjunto A en (2)), se llama dominio de la función, mientras que el conjunto de valores de la función se llama rango o condominio de la función.
Si todo elemento de B es el valor de la función para algún elemento de A, decimos que se trata de una función suprayectiva. Si A y B son el mismo conjunto, es decir, si se trata de una función suprayectiva de A en A, decimos que la función es una operación. Un ejemplo de operación tomado de la matemática, es 'x es el cubo de y’ una función de números en números. Si se proyectan los números naturales de 1 a n, siendo n un número cualquiera, en un conjunto A de objetos, tenemos una secuencia (en efecto, cada elemento de A recibe uno o varios números). Algunas funciones tienen más de un argumento. Consideremos, por ejemplo, un cuadro de distancias en millas entre las grandes ciudades del mundo. Puede parecerse a (4).
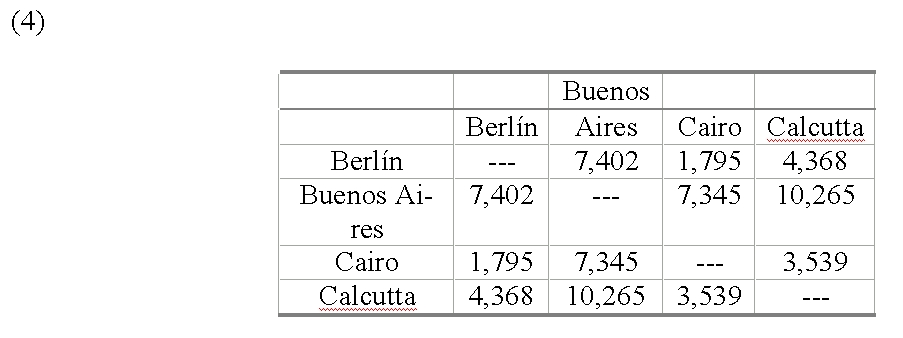
En este caso, la función toma pares de ciudades como argumentos y una distancia como valor.
Concluimos este capítulo mencionando un tipo peculiar de función que nos será de utilidad más tarde. Sean dos conjuntos A y B tales que B es un subconjunto de A. A puede ser el conjunto de los miembros del Parlamento y B el conjunto de los miembros del partido, mayoritario. Consideremos ahora un tercer conjunto C que contiene exactamente dos elementos, por ejemplo, los números 1 y 0. Podemos hora construir una función que asigne un 1 a todo elemento de A que sea también elemento de B y un 0 a todo elemento de A que no lo sea de B, es decir, a todo elemento que pertenezca al complemento de B relativo a A. Tal función se llama función característica del conjunto B relativo al dominio A.
La elección del conjunto C, de dos elementos, es de hecho arbitraria: cualquier par de objetos vale, siempre que se distingan de los elementos del conjunto que queremos diferenciar de su complemento. Es normal, en lógica, identificar los valores de verdad 'verdadero' y 'falso' (sobre los que volveremos en la sección 3.4) con los objetos utilizados como rango de la función característica.
1. Simbolizar:
(a) b es un elemento de C
(b) C es un subconjunto propio de D
(c) la unión de A y C
(d) el conjunto formado por los elementos d, e y g
(e) d no es un elemento de la intersección de A y B.
(f) el complemento de A es un subconjunto propio de la unión de B y C
2. Traducir las siguientes expresiones al castellano
(a) {x/x es un mozo y María a besado a x}
(b) {x/x es danés} Ç {x/x es filósofo}
3. ¿Cuál es el conjunto potencia de {Londres, Barcelona, Sevilla}?
4. Dado el siguiente diagrama:
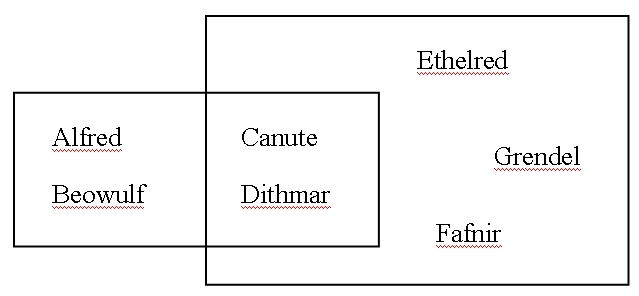
¿Cuál de las siguientes afirmaciones es verdadera y cuál falsa?
(a) Alfred es un elemento de A È B
(b) Alfred es un elemento de A Ç B
(c) A ÇB tiene dos elementos
(d) {Etheldered, Fafnir} Ì (A,u B)
(e) { Etheldered, Fafnir, Grendel } Ì (B ¾ A)
{Etheldered, Fafnir, Grendel} Í (B ¾ A)
5. Sombrear el área correspondiente al conjunto C(A Ç B)
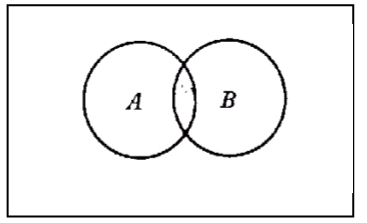
6. ¿Qué afirmaciones son verdaderas y cuáles falsas?
(a) c Î {a, b, c}
(b) d Ï {a, b, c}
(c) {a, b, c} Ì {a, b, c}
(d) {a, b, c} Í {a, b, c}
(e) {a, b} Í {a, b, c}
(f) c Î {b, {c}}
(g) {c} Î {b, {c}}
7. Indicar los dominios y codominios de las siguientes funciones:
(a) 'la capital de'
(b) 'la mujer de' (en una sociedad monógama)
(c) 'el jefe de Estado de'