Lógica de enunciados
Pulsar aquí para revisar el listado de SÍMBOLOS
Las relaciones lógicas entre los enunciados compuestos y los enunciados simples que los forman están determinadas, en general, por ciertas palabras llamadas conectivas enunciativas (o proposicionales). Las conectivas proposicionales pertenecen habitualmente a la categoría gramatical tradicional de las conjunciones (y, o, por lo tanto, porque, ya que, pero, antes que, como, aunque, si... entonces).
(1) Luis es un sindicalista aunque lea a Pemán
(2) Luis es un sindicalista aunque y lee a Pemán
(3) Luis es un sindicalista o lee a Pemán
El hecho de que realmente estemos tratando con relaciones lógicas diferentes se ve de modo particularmente claro si observamos las conclusiones podemos sacar de los tres enunciados. De (1) se sigue más o menos que no es de esperar que un sindicalista lea a Pemán. De (2) y (3) no se sigue tal conclusión. (3) no implica siquiera que los dos enunciados componentes sean verdaderos, sino sólo que al menos uno de los dos
La forma lógica definida por las conectivas determina, por lo tanto, las consecuencias lógicas que se siguen de los enunciados formados por medio de conectivas y otros enunciados.
Dado que al hacer lógica proposicional no estamos interesados en la estructura interna de los enunciados sino sólo en las relaciones lógicas entre ellos, introducimos las llamadas variables de enunciado (o proposicionales), esto es, signos que se refieren a cualquier enunciado. Habitualmente se utilizan como variables letras latinas minúsculas a partir de p. Utilizando variables de enunciado, nuestros anteriores ejemplos tendrían el siguiente aspecto.
(1’) p aunque q
(2’) p y q
(3’) p o q
En este momento estamos utilizando variables para los enunciados pero mostramos la estructura lógica con palabras. Sean cuales sean los enunciados que las variables representan, la estructura lógica continúa siendo la misma, puesto que depende sólo de las propiedades de las conectivas y no del contenido de los enunciados simples.
En lógica, los signos que tienen un significado permanente, no variable, se llaman constantes. Puesto que los functores o conectivas tienen esta propiedad y además forman parte de lo que hemos llamado vocabulario lógico, se llaman constantes lógicas, es decir, signos que por su significado y función permanente determinan la estructura lógica de los enunciados en los que aparecen. Las variables indican el contenido que se estructura y las constantes representan la estructura misma. Además de las conectivas proposicionales, se consideran constantes lógicas los cuantificadores y los operadores modales (todos los cuales estudiaremos luego).
Tradicionalmente se ha mostrado interés, en la lógica proposicional, por sólo cuatro de las conectivas del lenguaje natural, en concreto por las cuatro conectivas y, o, si... entonces y si y sólo si (si es que la última se puede considerar una conectiva en el lenguaje natural). También se ha estudiado cómo afecta la negación (no) a los enunciados.
La mayoría de las conectivas del lenguaje natural no se han estudiado. Conjunciones como por lo tanto, ya que, mientras, aunque y antes se han estudiado muy poco desde el punto de vista de su contribución a la estructura lógica de los enunciados.
Ha habido dos razones para ello. La primera y quizá principal es que la lógica se ha estudiado hasta ahora fundamentalmente por su interés matemático, lo que ha llevado a concentrarse en aquellos tipos de inferencia que son más comunes en el razonamiento matemático. Muchos de los tipos de razonamiento que realizamos en el lenguaje natural están por ello relativamente poco explorados.
La otra razón es más seria desde un punto de vista teórico. Se trata de la cuestión de si, y en qué medida, las conectivas del lenguaje natural son veritativos‑funcionales. Para entender esta cuestión, hemos de introducir el término valor de verdad. Todo enunciado tiene un valor de verdad y sólo uno. Un enunciado verdadero tiene el valor de verdad ‘verdadero’, mientras que un enunciado falso tiene el valor de verdad ‘falso’. Abreviamos los dos valores de verdad por medio de t y f, respectivamente. Consideremos el siguiente ejemplo.
(4) Hace un día templado y ventoso
(4) se puede parafrasear de modo lógicamente más transparente como sigue
Para que la expresión (4’) sea verdadera tanto (5) (a) como (5) (b) han de serlo.
(5) (a) Hace un día templado
(b) Hace un día ventoso
Sólo cuando los dos enunciados simples unidos por y son verdaderos, es verdadero también el enunciado compuesto, Si uno de los enunciados, o los dos, es falso, la expresión compuesta es falsa. Podemos decir, entonces, que el valor de verdad de la expresión compuesta es función de los valores de verdad de los enunciados simples.
Es veritativo‑funcional toda conectiva que tiene la propiedad de determinar el valor de verdad de la expresión compuesta en sola dependencia de los valores de verdad de los enunciados simples unidos por ella. Podemos expresar esto de manera diferente con la ayuda de los dos esquemas siguientes.
(6) (a) _____ y _______
(b) _____ o _______
Utilizamos aquí líneas en vez de variables. Tanto y como o son veritativo‑funcionales y por lo tanto el valor de verdad de los enunciados compuestos que forman están totalmente determinados por los valores de verdad de los enunciados que puedan reemplazar a las líneas.
Uno de los objetivos tradicionales de la lógica ha sido el de mostrar qué conclusiones podemos sacar correctamente de un conjunto de premisas, o, en otras palabras, qué conclusiones preservan la verdad de las premisas. Tiene por lo tanto grave importancia el entender las propiedades veritativo‑funcionales de las conectivas. Estas propiedades son lo que nos permite juzgar sobre la validez de un razonamiento, en la medida en que ésta es independiente de la verdad de hecho de los enunciados simples.
No todas las conectivas son veritativo‑funcionales. Veamos primero las diferencias entre los siguientes enunciados.
(7) Hay tormenta y me siento bien
(8) Hay tormenta pero me siento bien
(9) Dado que hay tormenta, me siento bien
Tanto y como dado que piden que los enunciados simples que combinan sean verdaderos para que la expresión compuesta que crean lo sea. Si esta condición se cumple, el enunciado con y es verdadero, pero no ocurre necesariamente lo mismo con dado que. El enunciado puede ser falso. Más allá de la conexión veritativo‑funcional entre los dos enunciados, dado que requiere que uno de ellos sea la razón del otro. Es decir, es necesario pero no suficiente que los dos enunciados simples sean verdaderos para que el enunciado compuesto con dado que sea verdadero. Dado que no es, por lo tanto, veritativo funcional.
Si nos volvemos a y y pero, vemos que el enunciado con pero es verdadero si los enunciados simples que une lo son. Así pues, pero es veritativo‑funcional. De todos modos, continúa existiendo una diferencia entre y y pero, aunque la diferencia no es veritativo‑funcional y la lógica, en su desarrollo actual, no tiene un método para tratarla. Todas las relaciones formales entre enunciados que se tratan en la lógica proposicional son veritativo‑funcionales.
Como hemos visto la lógica de enunciados tradicional está limitada por dos factores: sólo se han estudiado conectivas veritativo‑funcionales y, entre ellas, sólo han sido analizadas sistemáticamente las que son relevantes desde un punto de vista matemático. El lógico considera sin importancia la introducción de más conectivas veritativo‑funcionales, dado que se conoce el número, más bien pequeño, de funciones de verdad y que, además, toda función de verdad se puede reducir a combinaciones de operaciones con una sola función, a saber, la llamada barra de Sheffer, que se escribe ½ (p½q se lee ‘no p o no q’).
Originariamente la lógica se entendió como un instrumento de estudio de las propiedades lógicas del lenguaje natural. Se esperaba que traduciendo razonamientos en lenguaje natural el cálculo proposicional aparecerían aquellos en forma más clara, con lo que se haría más fácil ver si eran válidos. La traducción, sin embargo, no resultó fácil; había que traducir el lenguaje natural, con toda su ambigüedad y vaguedad, a un sistema de representación formal no ambiguo escogido, en cierta manera, arbitrariamente. Dado que tal sistema presentaba grandes ventajas en otros aspectos, la lógica se fue separando más y más del estudio del lenguaje natural. Todavía no hemos descubierto una manera mejor de estudiar y formalizar las relaciones no veritativo‑funcionales, aunque, el estudio de la pragmática, que plantearemos con cierta extensión en el capítulo 9, quizá ofrece un tipo de solución a este problema.
4.2. EL SIGNIFICADO DE LAS CONECTIVAS LOGICAS
Vamos ahora a estudiar un poco más de cerca el significado de las cinco conectivas que se usan normalmente en lógica proposicional. El requisito de que las conectivas sean veritativo‑funcionales implica que tengan, en lógica, un significado definido y fijo que sólo parcialmente coincide con su uso en el lenguaje ordinario. En las secciones siguientes apuntaremos algunas de las diferencias entre su significado en lenguaje natural y en lógica. Las cinco conectivas son: conjunción (y), disyunción (o), implicación (si... entonces), equivalencia (si y sólo si) y negación (no), que en realidad no es una conectiva, puesto que no une enunciados sino que opera sobre un sólo enunciado cada vez. Las cinco conectivas se representan en lógica con símbolos especiales.
Las siguientes expresiones corresponden normalmente en el lenguaje natural a la negación lógica.
(1) (a) Es falso que
(b) No es el caso que
(e) No
(d) No es exacto que
(e) Es falso que
La negación se usa en lógica para formar un enunciado compuesto cuyo valor de verdad es el contrario del enunciado simple sobre el que opera. Así, si Está nevando es verdadero, No está nevando ha de ser falso, y al revés. De manera abreviada esto puede expresarse como sigue. Usaremos variables de enunciado y un símbolo especial para no, ~ (¾ existe aunque menos corrientemente).
(2) p ~ p
t f
f t
Una abreviatura de este tipo, en la que se indican los valores de verdad de ~ p (el enunciado, compuesto) en dependencia de los valores de verdad de p (el enunciado simple) se llama tabla de verdad.
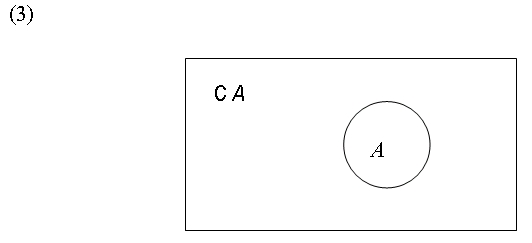
Podemos también caracterizar la negación en términos de teoría de conjuntos. Considérese (3). Sea A el conjunto‑verdad de p, es decir, el conjunto de mundos en los que p es verdadero. El conjunto‑verdad de ~ p será el conjunto de mundos en que p es falso, que coincide desde luego con CA, es decir, con el complemento de A.

Como ya hemos dicho, la negación lógica no es el equivalente de las expresiones de negación en el lenguaje natural. El lenguaje ordinario parece permitir la aparición de negaciones en el interior del enunciado, pero esto no es posible en lógica proporcional.
(4) No se permite la entrada a los no estudiantes
Hemos de ignorar la negación que precede a ‘estudiantes’ y traducir (4) como ~ p. Otra diferencia es que la posibilidad de hacer hincapié, por medio del énfasis y la entonación, en los diferentes constituyentes de un enunciado negado, se pierde en la lógica proporsicional. Compárese (5) y (6).
(5) María no besó a Pepe
(6) Mari no besó a Pepe
(5), si se dice con el acento y entonación normales, es la negación neutral de Mari besó a Pepe, mientras que (6), en donde se enfatiza Mari, parece presuponer que fue otra quien besó a Pepe. La diferencia entre (5) y (6) no puede reproducirse en lógica proposicional; ambas expresiones se traducirían como ~ p.
(7) D. Gil Calzasverdes no creía que a Alfredo le gustaran los pasteles
Finalmente, (7) es ambiguo para mucha gente, puesto que existe la posibilidad de entender que la negación afecta o bien a la oración principal o bien a la subordinada. No es posible reproducir tales complejidades en la representación formal de la lógica proposicional.
La conjunción se asemeja al y del lenguaje cotidiano. La conjunción se usa en lógica para construir un enunciado compuesto que es verdadero sólo si son verdaderos los enunciados simples a partir de los cuales se forma el compuesto. Si alguno de los enunciados simples es falso, el enunciado compuesto o conjunción (es costumbre usar el nombre de la constante lógica para designar también la expresión compuesta que crea) es también falso. Así (1) es verdadero, mientras que (2) es falso.
(1) El fuego quema y Carnap fue filósofo
(2) El fuego quema y Carnap fue torero
Podemos resumir esto en una tabla de verdad con variables de enunciado y & como símbolo de la conjunción.
(3)
p q p & q
t t t
t f f
f t f
f f f
Vemos que hemos agotado todas las posibilidades de, combinar los valores de verdad de p y de q y que sólo si ambos elementos de la conjunción son verdaderos, lo es también la conjunción en su conjunto.
Estudiemos ahora la relación entre el conjunto‑verdad de p & q y el conjunto‑verdad de los enunciados simples que contiene. En (4) A es el conjunto‑verdad de p y B es el conjunto‑verdad de q.
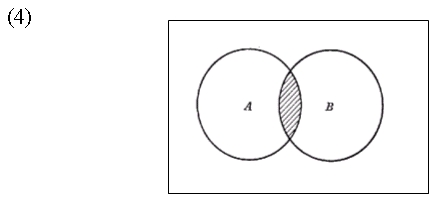
El conjunto‑verdad de p & q es el conjunto de mundos en que tanto p como q son verdaderos. Es decir, la intersección de A y B. Se puede decir de modo general que el conjunto‑verdad de una conjunción es equivalente a la intersección de los conjuntos‑verdad de los enunciados simples que forman parte de la conjunción. Una manera diferente de ver las relaciones entre conjunción e intersección puede ser la siguiente. Supongamos que Emilio (e) es miembro de un club de ajedrez A y de un club de fútbol B. En tal caso es verdad que e ÎA & e Î B. Sabemos que una conjunción es verdadera sólo si son verdaderos los dos enunciados de que está compuesta.
(5) e Î A & e Î B
t t t
t f f
f f t
f f f
Así pues, sólo en el caso de que e sea miembro tanto de A como de B, o en otras palabras, de que sea un elemento de la intersección de A y B, será verdadera la conjunción compuesta e ÎA y e Î B.
Al igual que hemos visto en el caso de la negación, el significado de la conjunción lógica es algo diferente del y del lenguaje cotidiano. Mientras que & sólo se puede usar para unir enunciados, y se utiliza para unir constituyentes en el interior de los enunciados. El y de Juan y Pepe no puede traducirse. Sólo si los términos se pueden distribuir en enunciados diferentes se hace posible la traducción en un enunciado compuesto.
(6) se puede dividir en dos enunciados (véase (7)) si Juan y Pepe tiene cada uno un coche.
(6) Juan y Pepe tienen un coche
(7) Juan tiene un coche y Pepe tiene un coche (p & q)
Sin embargo, si son los dueños de un solo coche, no es posible un análisis del tipo de (7) y basta p como traducción.
Las oraciones unidas por y en lenguaje ordinario expresan a menudo una sucesión de hechos. Si se cambia el orden de los elementos de la conjunción, cambia con él el orden de los sucesos.
(8) Gunnar se tumbó en el lecho y murió
(9) Gunnar murió y se tumbó en el lecho
En lógica p & q es siempre equivalente a q & p. La conjunción lógica, se ve en la comparación de (8) con (9).
Hay otros muchos usos de y en el lenguaje cotidiano. A menudo ocurre que no deben analizarse como conjunciones lógicas.
(10) Tócame y te beso
(11) Corre un kilómetro diario y te sentirás un hombre nuevo
(10) y (11) deberán probablemente analizarse como implicaciones y no como conjunciones.
(10) (a) Si me tocas, entonces te beso
(11) (b) Si corres un kilómetro diario, entonces te sentirás un hombre nuevo
En lógica de enunciados es habitual admitir sólo conjunciones de dos enunciados. En el lenguaje ordinario no existe tal limitación, p. ej.
(12) Julio fuma y Octavio va de fulanas y Antonio bebe y Cleo se lamenta
Nada hay que impida la construcción de una lógica de enunciados que opere de esta manera, es decir, permitiendo que la conjunción una más de dos enunciados. En este caso resulta práctico poner & delante de los enunciados que se han de combinar y escribir la expresión del siguiente modo: & (p, q, r, s, t, u, v, w). Este método de escritura (la llamada notación polaca, que introduciremos en uno de los ejercicios) puede, naturalmente, utilizarse también cuando, sólo se unen dos enunciados. Todo esto vale también para nuestra próxima conectiva, la disyunción. Además hay que tener en cuenta que ((p & q) & r) es lógicamente equivalente a (p & (q & r)), lo que significa que toda conjunción, independientemente de su tamaño, puede reducirse a una cadena de conjugaciones binarías (en terminología matemática decimos que la conjunción es asociativa).
La disyunción corresponde muy exactamente al o del lenguaje ordinario. La disyunción se utiliza en lógica para crear un enunciado compuesto (llamado también disyunción) que es falso sólo si los dos enunciados simples que lo forman son falsos. Basta, pues, conque uno de los enunciados que forman la disyunción sea verdadero para que la disyunción completa lo sea. Así, dado el actual estado de nuestros conocimientos, (1) es falso y (2), verdadero.
(1) Marte es un satélite o un agujero negro
(2) Marte es un planeta o un agujero negro
La tabla de verdad para la disyunción, con el símbolo especial Ú, es la siguiente.
(3) p q pÚq
t t t
t f t
f t t
f f f
Vemos que una disyunción es falsa si los dos enunciados que la forman lo son; en otro caso es verdadera.
En la sección precedente vimos que la conjunción corresponde a la intersección conjuntista. Estudiemos ahora la disyunción. Sean de nuevo A y B en (4) los conjuntos‑verdad de p y q respectivamente.
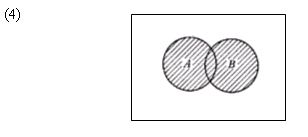
El conjunto‑verdad de p Ú q es el conjunto de mundos en que p o q son verdaderos, o lo que es lo mismo, la unión de A y B. El conjunto verdad de una disyunción es, por lo tanto, equivalente a la unión de los conjuntos‑verdad de los enunciados simples con los que se forma.
Podemos demostrar la conexión entre unión y disyunción de un modo distinto. Supongamos que sabemos que Emilio (e) es miembro de un sólo club o de los dos. En este caso será verdadero lo siguiente:
e Î A Ú e Î B. Vemos que la disyunción de los enunciados e ÎA y e ÎB es verdadera sólo si e es elemento de la unión de A y B.
Otra vez encontramos aquí discrepancias entre la disyunción lógica y el uso de o en el lenguaje natural.
A menudo se indica, con el o del lenguaje ordinario, un tipo más estricto de disyunción, que sólo es verdadero si exactamente uno de los elementos de la disyunción lo es. Para esta conectiva se utiliza a menudo un signo propio, xxx, y se llama disyunción exclusiva, para distinguirla de Ú, disyunción inclusiva. La disyunción exclusiva tiene la siguiente tabla de verdad.
(5) p q p xxx q
t t f
t f t
f t t
f f f
En este caso la disyunción es falsa si los dos enunciados que la forman son verdaderos o si los dos son falsos. El o exclusivo es veritativo‑funcional, pero no es el o que se utiliza primordialmente en lógica. La razón es que podemos representar el o exclusivo usando y, no y el o inclusivo de la siguiente manera.
(6) (p Ú q)& ~ (p& q)
Partiendo del o inclusivo, excluimos la posibilidad de que tanto, p como q sean verdaderos negando la conjunción que afirma que tanto p como q son verdaderos. Esta es justamente la función del o exclusivo. Encontramos un o que parece funcionar como una disyunción exclusiva en enunciados y formados con o bien... o bien... y en preguntas y peticiones.
(7) O bien Dios es bueno o bien no lo es
(8) ¿Quieres vino blanco o tinto?
(9) i La bolsa o la vida!
Un o con carácter más claramente inclusivo lo encontramos en (10), donde, naturalmente el caso normal es que los dos elementos de las disyunción sean verdaderos de una persona.
(10) Todo aquel que es ciudadano sueco o ha vivido en Suecia durante el año precedente está obligado a hacer declaración de renta.
Hay que hacer notar que el aire de incertidumbre que en la conversación normal acompaña al uso de o no es necesario en lógica. Por lo que a la lógica toca es perfectamente aceptable usar el siguiente enunciado mientras que se mira como cae la primavera nevada del invierno
(11) Está nevando o está lloviendo
Lo único que se precisa para que una disyunción sea verdadera es que lo sea de uno de los enunciados que la forman. Este es el caso en la situación descrita, aunque esté totalmente excluido que esté lloviendo.
Normalmente, sin embargo en la comunicación lingüística intervienen muchas más cosas que propiedades veritativo‑fundamentales. El hecho de que (11), pronunciado en la situación antes descrita, se consideraría como una expresión en cierto modo extraña, muestra que además de las propiedades veritativo‑funcionales hay otros factores que determinan nuestra interpretación de los hechos lingüísticos.
Como sugestión para un análisis de estos factores podemos decir que hay un conjunto de normas comunicativas que tienden a hacer lo más efectivo posible el intercambio de comunicación entre los participantes en un diálogo. Basándonos en esas normas se podría decir: no se debe decir p Ú q si se puede decir p o p & q, que son expresiones que conllevan más información definida, por virtud de sus tablas de verdad. Las expresiones lingüísticas deberían utilizarse del modo más efectivo posible, logrando que tanto, lo que se dice corno lo que no se dice tenga relevancia para el modo de entender lo dicho. Este es uno de los supuestos normalmente implícitos en la comunicación lingüística.
La implicación de la lógica de enunciados es todavía más diferente de las expresiones correspondientes en el lenguaje ordinario (si... entonces, si y, a veces, y) que las otras conectivas que hemos estudiado. Consideremos algunos ejemplos de si... entonces en el lenguaje ordinario.
(1) Si has trabajado mucho (entonces) probablemente estés cansado
(2) Si está lloviendo (entonces) habrá humedad
(3) Si Hengist es más gordo que Horsa (entonces) Horsa es más delgada que Hengist
(4) Si eres buen chico (entonces) tendrás pastel
En (1) y (2), si... entonces indica una ‘ligazón causal’ entre el antecedente y el consecuente. En (4), el antecedente está ligado al consecuente por la obligación de una promesa por parte del hablante. Podemos decir que en (3) si... entonces expresa una consecuencia lógica. La lógica proposicional trata la implicación sólo desde el punto de vista veritativofuncional, y por ello simplemente estipula que una implicación es verdadera cuando su antecedente es falso o su consecuente verdadero. Podemos dar, por lo tanto, la siguiente tabla de verdad para la implicación. Como símbolo utilizamos®. (Quizá es más corriente usar É, pero se confunde con facilidad con Ì, el símbolo de la inclusión en teoría de conjuntos).
(5) p q p®q
t t t
t f f
f t t
f f t
La implicación veritativo‑funcional se llama habitualmente implicación material y, como vemos, sólo es falsa cuando el antecedente es verdadero y el consecuente falso. Veamos ahora qué correspondencias hay entre la implicación material y el uso del si... entonces en el lenguaje ordinario.
Hay un caso que parece presentar pocos problemas: una oración con si... entonces es falsa, al igual que un enunciado con ®, cuando su antecedente es verdadero y su consecuente falso. Así, en (6).
Quizá es también natural decir que la implicación (el enunciado compuesto) es verdadero cuando tanto el antecedente como el consecuente lo son. Sin embargo lo normal es que se exija algo más de un enunciado formado con si... entonces en la conversación normal. Habitualmente se requiere que el antecedente y el consecuente estén ligados por alguna relación que no es veritativo-funcional, como, por ejemplo, una relación causal o de consecuencia lógica. Véanse los ejemplos 1‑4). Consideremos el enunciado /7(.
En este caso antecedente y consecuente no guardan ninguna relación entre sí, pero ambos son verdaderos y como los valores de verdad son lo único relevante en una evaluación veritativo‑funcional de un enunciado compuesto, (7) ha de tratarse exactamente del mismo modo que el resto de los enunciados con si... entonces, en los que además de tener un antecedente y un consecuente verdaderos, existe algún tipo de relación no veritativo‑funcional entre ellos.
La situación empeora cuando el antecedente de una implicación es falso. Veamos una apuesta.
(8) Te apuesto a que si llueve, mañana no habrá excursión
Si la condición de que llueva no se cumple, la apuesta no vale, es como si no hubiera apuesta Parece natural pensar que esto ocurre también en el caso de enunciados puros.
(9) Si los perros son peces, entonces no pueden nadar
En cualquier caso no parece tener sentido decir que algo acerca del valor de verdad de la implicación cuando el antecedente es falso. Hay ejemplos de este tipo (llamados habitualmente enunciados contrafácticos) que son todavía más claramente absurdos.
(10) Si fuera invisible, todo el mundo me vería
Supongamos que (10) se analiza en la forma p ® q y que p es falso, cosa que es demostrable empíricamente. En este uso p®q es automáticamente verdadero, por las condiciones de verdad de la implicación.
(11) Si fuera invisible, nadie me vería
(11) que parece mucho más razonable sería verdadero por la misma razón. No hay modo de dar cuenta de nuestra intuición de que (11) parece bastante razonable, mientras que (10) parece totalmente absurdo. Los dos enunciados se analizan como p ® q y se tratan de la misma manera desde el punto de vista veritativo‑funcional.
(12) Si Daoiz y Velarde eran franceses, entonces eran valientes
(13) Si Daoiz y Velarde eran franceses, entonces no eran valientes
Aunque (13) dice lo contrario de (12), hay que considerar verdaderos a ambos si analizamos el antecedente y el consecuente como unidos por la implicación material, dado que el común antecedente de ambos es falso.
Aunque el análisis de si... entonces como implicación material es inadecuado en muchos aspectos, hay unas cuantas cosas que hablan a su favor. Parece que los enunciados en lenguaje ordinario que corresponden a expresiones lógicas veritativo‑funcionalmente equivalente a p®q, tienen muy aproximadamente el mismo alcance que las expresiones del lenguaje ordinario que corresponden a p®q. ~p Ú q es equivalente, desde el punto de vista veritativo‑funcional, a p ® q. Las tablas de verdad nos dicen que la implicación material es verdadera si su antecedente es falso o su consecuente verdadero. Esto es exactamente lo que expresa ~p Ú q ‘antecedente falso o consecuente verdadero’. Podemos comprobarlo construyendo la tabla de verdad de ~p Ú q.
(14) y (15) corresponden en el lenguaje ordinario a p ® q y ~p Ú q, respectivamente.
(14) Si estoy en lo cierto, te debo 10 duros
(15) 0 estoy equivocado o te debo 10 duro
Como vemos tienen el mismo significado Esto resta cierto apoyo in directo al análisis veritativo‑funcional de si... entonces que hemos estipulado. Ha habido también intentos de usar la implicación material como base de un análisis de si... entonces que utiliza normas comunicativas del tipo que mencionamos antes al hablar de la disyunción. Los antedichos resultados del análisis de si... entonces como ®, en cierto modo absurdos, se explican desde esta perspectiva como violaciones de normas comunicativas generales.
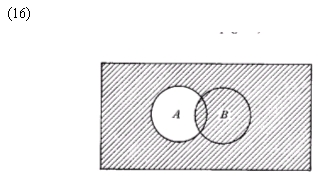
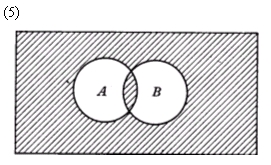
La contrapartida conjuntista de la implicación no es tan directa como las que hemos estudiado para las otras conectivas. En (16), A y B son los conjuntos‑verdad de p y q, respectivamente y el área sombreada, el conjunto‑verdad de p®q.
La equivalencia corresponde aproximadamente a si y sólo si, justamente cuando, sólo cuando, sólo si. A veces incluso se utiliza un simple si para indicar la equivalencia. En cuanto función de verdad, una equivalencia se analiza como una doble implicación material, una que va de antecedente a consecuente y otra de consecuente a antecedente. Dado, que el análisis de la equivalencia se basa en el de la implicación, algunos de los problemas de la correspondencia entre implicación y lenguaje ordinario vuelven a aparecer en conexión con la equivalencia.
Otro problema que, en ocasiones, es causa de dificultades, es el de diferenciar entre equivalencia e implicación. Intentaremos clarificar la distinción con dos ejemplos.
(2) Mari pasará el examen si y sólo si el resultado de su ejercicio escrito es satisfactorio
En (1), ‘pasar el ejercicio escrito’ es una condición suficiente pero no necesaria para que Mari pase el examen. Exámenes orales, rojas manzanas o incluso un leve coqueteo pueden ser otros medios suficientes. En (2), sin embargo, pasar el ejercicio escrito no es sólo una condición suficiente sino también necesaria para pasar el examen. No hay otros medios.
Dado que la equivalencia es una conjunción de dos implicaciones, obtenemos la siguiente tabla de verdad para la equivalencia. Como símbolo especial usamos º (a veces se usa « o xxx ). Muy frecuentemente ‘si y sólo si’ se abrevia en ‘sii’.
(3) p q p º q
t t t
t f f
f t f
f f t
Como vemos, la equivalencia es verdadera sólo cuando los enunciados simples que la forman tienen el mismo valor de verdad. Si pensamos en la equivalencia como en una conjunción de dos implicaciones materiales, entenderemos por qué es así.
(4) (p®q) &(q®p)
Sabemos que para que una conjunción sea verdadera se precisa que todos los enunciados que la forman sean verdaderos. Para que esta condición se cumpla o bien p y q son ambos verdaderos o bien son ambos falsos. Si tienen diferentes valores de verdad, las condiciones de verdad de la implicación material no se cumplirá en los dos enunciados simultáneamente (el antecedente puede no ser verdadero y el consecuente falso), que es lo que se precisaría para que la conjunción fuera verdadera.
La contrapartida conjuntista de la equivalencia es bastante clara y muestra que se mantiene la condición de simultaneidad del valor de verdad de los dos enunciados. En (5) el conjunto‑verdad de p º q está sombreado, mientras que A y B representan los conjuntos‑verdad de p y de q respectivamente.
Tanto en lógica como en lingüística es de gran importancia saber qué estructura tiene una secuencia de símbolos, qué elementos de la secuencia están relacionados entre sí y cuáles no. Hay muchos métodos de representar la estructura lingüística por medio de diagramas. Los más comunes son los diagramas arbóreos, los diagramas cuadrados y los paréntesis. Formalmente son equivalentes, pero difieren en cierta medida en su aplicación práctica. El método habitual, en lógica, de indicar la estructura son los paréntesis.
La razón más importante, en lógica, para señalar la estructura constitutiva es evitar ambigüedades. Sin indicación de cuál es su estructura, la siguiente expresión es, inevitablemente, ambigua.
(1) Que nieva y llueva implica que habrá humedad y hará frío
(2) p &q®r &s
Existen entonces las siguientes posibilidades de entender la implicación
(3) (p & q) ® (r & s)
(4) P & (q ®(r & s))
(5) P & ((q® r) & s)
(6) ((P & q) ® r) & s
Las diferentes estructuras que hemos indicado con paréntesis en (3)‑(6) también pueden ponerse ‑de manifiesto con diagramas arbóreos y cuadrados.
DIAGRAMAS ARBÓREOS. Daremos primero los árboles sin rotular las ramificaciones (una ramificación es una intersección de líneas en un árbol) y luego con ramificaciones rotuladas. Los rótulos de las ramificaciones se abrevian como sigue: Implicación = Impl, Conjunción = Conj. La conectiva que está colocada directamente debajo de la ramificación más alta se llama conectiva principal del enunciado. En (3’) es la flecha de la implicación.
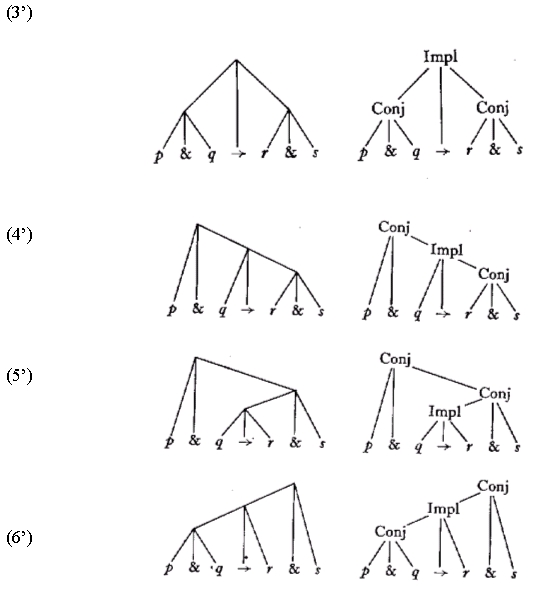
DIAGRAMAS CUADRADOS. En este caso ponemos rótulos en el diagrama desde el principio.
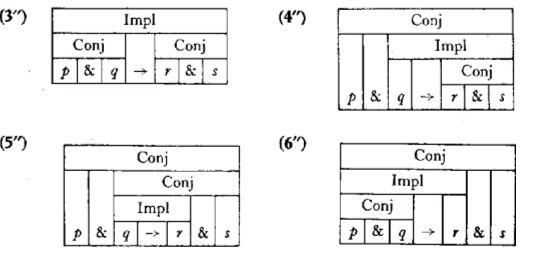
Los rótulos pueden usarse también, naturalmente, con paréntesis (tenemos entonces los llamados paréntesis rotulados). Abreviamos el término implicación por I y conjunción por C.
(3”’) (I(Cp & q) ® (cr & s)C)I
(4’’’) (Cp & (iq ®(Cr & s)C)I)C
(5’’’) (Cp & (c(Iq ® r)I & s)C)C
(6’’’) (C(I(Cp & q)C ® r)I & s)C
Antes de acabar esta digresión conviene decir que normalmente los paréntesis se usan en lógica sólo en la medida en que son necesarios para lograr claridad. A menudo se utilizan las siguientes convenciones: si un signo de negación es siempre el menor posible, es decir, la negación se aplica al constituyente más pequeño que esté a su derecha. En general, llamamos alcance de un operador lógico a las partes de una expresión a las que afecta el operador. El alcance se indica por contigüidad directa, como en el caso de la negación, o por paréntesis, en cuyo caso todo lo que está encerrado dentro de una pareja de paréntesis constituye el alcance.
(7) ~p & q
(8) ~ (p & q) & r
Así, en (7) la negación se aplica sólo a p y no a la conjunción completa, mientras que en (8) los paréntesis hacen que se aplique la negación a la conjunción más a la izquierda y no a la expresión entera. De modo semejante, se suele dar un alcance menor a & y a Ú que a ® y º Si aceptamos estas convenciones, nuestro ejemplo (2)
(2) p & q ® r & s
deja de ser ambiguo y ha de ser interpretado como (p & q) ® (r & s). De todos modos no vamos a seguir estas convenciones excepto en el caso de la negación, y usaremos paréntesis siempre que parezca necesario para evitar ambigüedades.
Hemos alcanzado el punto en el que podemos dar un resumen de los símbolos más simples de la lógica de enunciados. Podemos dar también un conjunto de reglas que nos dicen cómo se pueden combinar para formar unidades mayores. Las reglas tienen la propiedad de decir exactamente qué combinaciones están permitidas y cuáles no.
La enumeración de los símbolos simples pequeños se suele llamar, en lógica, vocabulario. Tiene la misma función que un diccionario para el lenguaje natural. Las reglas que definen las combinaciones permitidas de unidades simples ‑las llamadas expresiones bien formadas (ebf)- se suelen llamar reglas de formación y pueden compararse con las reglas gramaticales de un lenguaje. Vocabulario y reglas de formación forman la sintaxis de la lógica. La sintaxis no nos dice nada sobre cómo han de interpretarse signos simples y expresiones, es decir, qué significado tienen. Esto último constituiría el tema de la semántica.
Estamos ahora en situación de poder definir qué es un lenguaje formal. Un lenguaje formal es un conjunto de expresiones definido en relación con un vocabulario a partir del cual se forman las expresiones de acuerdo con las reglas de la sintaxis e interpretado por las reglas de la semántica. Ha de hacerse en este punto una importante distinción entre hablar EN un lenguaje de este tipo y hablar ACERCA de él. El lenguaje mismo—el objeto que investigamos‑ se llama lenguaje objeto y el lenguaje que usamos para estudiar el lenguaje objeto se llama metalenguale. Así pues, el lenguaje que usamos en gramática o en lógica para hablar acerca de otros lenguajes, se puede caracterizar como metalenguaje.
Al dar la sintaxis de la lógica de enunciados comenzamos por su vocabulario.
(i) Un número infinito de variables de enunciado: p, q, r, s, t, p1, q1,... p2, q2...
(ii) Las conectivas lógicas: ~, &, Ú, ®, º
(iii) Paréntesis: ( )
(iv) No hay otros signos en las expresiones de la lógica proposicional
En segundo lugar hemos de indicar qué combinaciones de signos están permitidas- qué expresiones están bien formadas-. Damos, pues, las reglas de formación en la lógica de enunciados.
(2) REGLAS DE FORMACIÓN
(i) Toda variable de enunciado es una ebf
(ii) Si a y b son cualesquiera ebfs., entonces (a) ~a, (b) (a & b) (c) (aÚ b), (d) (a®b) y (e) (aºb)
(iii) Una expresión está bien formada sólo si ha sido construida según estas reglas.
En la regla (ii) queremos dejar claro que estamos hablando, acerca de un lenguaje en un metalenguaje y por ello hemos introducido las llamadas metavariables (las letras griegas a, b) en vez de las variables de enunciado que cabría esperar. Hacemos esto para indicar que no estamos hablando de enunciados SIMPLES cualesquiera sino de cualquier ebf, es cogida arbitrariamente, de la lógica de enunciados a y b pueden ser sustituidas por cualquier ebf. Por lo tanto las reglas de formación pueden aplicarse sobre sus propios resultados. Consideremos, por ejemplo, las ebfs p y q. De acuerdo con la regla (ii) (b) podemos formar con ellas la ebf (p & q). Podemos aplicar la regla (ii) (b) de nuevo y obtenemos (p & q) & p. Como vemos, a se sustituye aquí por p & q, que es una ebf. De esta manera, aplicando, paso a paso les reglas, podemos generar expresiones tan largas y complejas como queramos. Las reglas que tienen esta propiedad se llaman recursivas y han jugado un gran papel en el desarrollo de la gramática generativa y de muchos lenguajes de computador. A menudo llamamos inducción (matemática) a la aplicación de reglas recursivas.
Al ser recursivas las reglas sintácticas, podemos construir un número indefinidamente amplio de expresiones por medio de un conjunto finito de reglas. Dado que todo lenguaje natural contiene un conjunto indefinido de oraciones gramaticalmente correctas, la gramática de un lenguaje natural tiene probablemente que contener reglas recursivas.
Las siguientes expresiones valen como ejemplo de ebfs. No utilizaremos aquí los paréntesis externos de la regla (ii), que fueron introducidos sólo para evitar ambigüedades: p, q, p & q, (p & q) ® q, p Ú q, (p & q) º º (p Ú q). Las siguientes expresiones no son ebfs: & q, Ú r ® q, q ~ ® p.
Las reglas (2) (i) y (2) (ii) pueden formularse, de modo equivalente, como sigue:
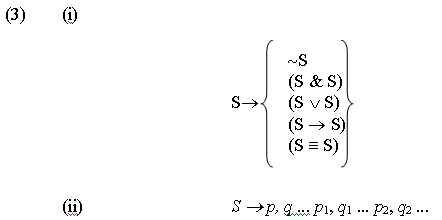
Escritas de esta manera, las reglas tienen la misma forma que las llamadas reglas de estructura de frase en la gramática generativa. Dado que en una gramática generativa la regla (2) (iii) se acepta por una convención implícita, las reglas (3) (i) y (ii) constituyen una descripción alternativa y equivalente de la sintaxis de la lógica proposicional.
Al describir la sintaxis de la lógica de enunciados hemos considerado los símbolos lógicos como si estuvieran ‘vacíos’, sin significado. Pero estamos interesados también, naturalmente, en utilizar la lógica para razonar sobre el mundo que nos rodea. Tan pronto como ponemos en relación los signos que hemos estado estudiando con los fenómenos que representan, damos el paso de la sintaxis a la semántica. La semántica es el estudio de cómo se relacionan las expresiones sintácticamente correctas con aquello de lo que tratan.
Dado que nuestro interés primordial en lógica está en los enunciados, vamos a estudiar el significado de los enunciados. Uno de los mejores medios para entender el significado de un enunciado es imaginar cómo tendría que ser el mundo para que el enunciado fuera verdadero.
(1) El Barón de Münchhausen se salió del agua estirándose de los pelos
La razón de que (1) sea difícil de entender es que uno no se imagina con facilidad cómo tendría que ser el mundo para que (1) fuera verdadero. El concepto de verdad nos da, pues, un instrumento preciso para captar la relación entre un enunciado y aquello de lo que trata. Podemos caracterizar una importante parte del significado de un enunciado formulando las condiciones que tendría que cumplir el mundo para que el enunciado fuera verdadero (en otras palabras, diciendo en qué mundos sería verdadero). Estas condiciones se llaman condiciones de verdad del enunciado. El significado de un enunciado se equipara, en lógica, con sus condiciones de verdad. Naturalmente, esto significa que hay importantes aspectos del significado que la lógica pasa por alto, pero un análisis del tipo indicado satisface ya las necesidades de la lógica, puesto que estamos interesados sólo en aquellos aspectos del significado que afectan a la verdad y a la inferencia lógicas.
La lógica de enunciados trata los enunciados simples como unidades no analizadas y por ello no podernos hablar, dentro de los límites de esa lógica, de las condiciones de verdad de los enunciados simples. Podemos, eso sí, decir bastantes cosas acerca de las relaciones entre las condiciones de verdad de los enunciados compuestos y las condiciones de verdad de los enunciados simples a partir de los cuales aquellos se forman.
Dicho con más precisión, en lógica proposicional estamos interesados en estudiar cómo se determina el valor de verdad de un enunciado compuesto a través del valor de verdad de los enunciados que lo constituyen y de las conectivas que en él aparecen. Así pues, el valor de verdad es aquí la única propiedad relevante de los enunciados simples. Para estudiar qué ocurre en los enunciados compuestos, lo habitual es atribuir arbitrariamente un valor de verdad a cada variable de enunciado. (Desde luego sería posible utilizar auténticos enunciados y comprobar el valor de verdad de cada enunciado, pero este procedimiento tendría un interés muy limitado, puesto que lo que nos interesa es el efecto de la conectiva sobre el valor de verdad del enunciado compuesto, dado, un conjunto cualquiera de valores de verdad de los enunciados constituyentes.)
Vamos a dar ahora las condiciones de verdad de los enunciados compuestos por medio de la información que nos ofrece la tabla de verdad de cada conectiva. Vamos a utilizar de nuevo letras griegas como metavariables para expresiones cualesquiera, lo que significa que nuestras condiciones de verdad serán recursivas. Se pueden aplicar una y otra vez para determinar las condiciones de verdad de expresiones cada vez más complejas. De ‘nuevo establecemos una diferencia entre el lenguaje de la investigación -el metalenguaje‑ y el lenguaje que investigamos ‑el lenguaje objeto. Estamos dando las condiciones de verdad del lenguaje objeto y no pretendemos ningún tipo de análisis del metalenguaje, del que simplemente suponemos que se entiende. El símbolo ‘ssi’ que utilizamos más abajo pertenece al metalenguaje—es parte de la descripción de las condiciones de verdad del lenguaje objeto‑ y debe, por lo tanto, diferenciarse de º, que es un símbolo del lenguaje objeto, el lenguaje que estudiamos. En (2) se definen, recursivamente, las condiciones de verdad de los enunciados compuestos de la lógica proposicional.
(2) SEMÁNTICA DE LA LOGICA PROPOSICIONAL
(i) ~ a es verdadero sii a no es verdadero
(ii) a & b es verdadero ssi tanto a como b son verdaderos
(iii) a Ú b es verdadero ssi al menos una de las expresiones a o b son verdaderas
(iv) a ® b es verdadero ssi a no es verdadero o b es verdadero
(v) a º b es verdero ssi a y b tienen el mismo valor de verdad
Por medio de estas condiciones de verdad podemos calcular el valor de verdad de una expresión por compleja que sea. Veamos algunos ejemplos.
(3) (p & (q v p)) ® (p v r) & q)
Vamos a suponer ahora que se han asignado valores de verdad a las variables, bien por medio de una asignación arbitraria, bien por sustitución de las variables por enunciados declarativos y posterior asignación de sus valores de verdad. Aceptemos que se han asignado a las variables los siguientes valores de verdad: p es verdadero, q y r son falsos. Representemos ahora el ejemplo en forma de diagrama como un árbol invertido, para ver cómo, los valores de verdad de las expresiones simples determinan el valor de verdad de la expresión compuesta. Disyunción, negación y equivalencia están abreviadas como ‘Disj’, ‘Neg’ y ‘Eq’ respectivamente; conjunción e implicación, igual que antes, como ‘Conj’ e ‘Impl’.
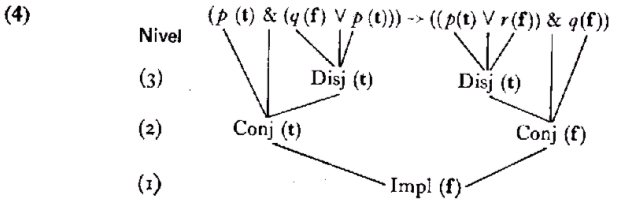
Las disyunciones de nivel (3) son ambas verdaderas, dado que al menos uno de los enunciados simples lo es. En el nivel (2) sólo la primera conjunción es verdadera, puesto que sus enunciados subordinados (uno de ellos, a su vez, compuesto) son verdaderos. La otra conjunción es falsa, pues uno de los enunciados que la forman es falso.
La implicación en el nivel (1) es falsa, puesto que su antecedente es verdadero y su consecuente falso. El valor de verdad de la expresión compuesta es, por lo tanto, f. Vale la pena hacer notar que al calcular el valor de verdad de la expresión compuesta hemos trabajado, por así decir, de dentro hacia fuera. Empezamos con los constituyentes menores, más internos, y terminamos con el mayor. ¡Los paréntesis de más adentro son lo primero! Quienes estén familiarizados con la gramática chomskyana en la versión de (1965) observarán que este principio se cumple también en las reglas cíclicas, en sintaxis y fonología, y en las reglas de proyección, en semántica. El ejemplo final es una equivalencia cuyo análisis dejamos como ejercicio al lector.
Hay ciertas expresiones compuestas que siempre reciben el valor de verdad ‘verdadero’ independientemente de los valores de verdad asignados a los enunciados simples de la expresión. Tales expresiones tienen un interés especial en lógica, puesto que puede decirse que su valor de verdad está determinado totalmente por las propiedades veritativo‑funcionales de las conectivas, es decir, por su forma lógica. Llamamos tautologías a este tipo de expresiones. Hay otras expresiones que tienen siempre el valor de verdad f como valor de verdad de la expresión entera. Son las llamadas contradicciones.
Las tautologías, por ser siempre verdaderas, son verdades lógicas. Hay, sin embargo, verdades lógicas que no son tautologías, como veremos luego. Del mismo modo que el concepto de verdad lógica es más amplio que el de tautología, el de verdad analítica es más amplio que el de verdad lógica.
La disyunción de un enunciado con su propia negación vale como ejemplo sencillo de tautología.
(1) p Ú ~ p (Está lloviendo o no está lloviendo)
Sea cual sea el enunciado p y su valor de verdad, el valor de verdad de la expresión compuesta será siempre t; es decir, estamos ante una verdad lógica. Otra manera de plantear esta idea consiste en decir: ‘Por mucho que el mundo cambie (sea el que sea el mundo que escojamos), la luna es un pedazo de queso verde o no lo es’. En otras palabras, el conjunto‑verdad de una tautología es siempre el conjunto de todos los mundos posibles (el conjunto universal): es fácil ver que el conjunto de mundos posibles en que p ~Ú p es verdadero es la unión del conjunto de mundos en que p es verdadero y del conjunto de mundos en que ~ p es verdadero, o lo que es lo mismo, el conjunto universal. Se puede decir de modo general que el conjunto‑verdad de una tautología es el conjunto universal y que el conjunto‑verdad de una contradicción es el conjunto vacío.
Sería bueno tener un procedimiento mecánico para decidir si un enunciado es una tautología o no. En lógica de enunciados existe un procedimiento así. Es el método de las tablas de verdad.
Hemos usado este método, de modo parcial, al estudiar las propiedades veritativo‑funcionales de las conectivas. Ahora vamos a ver cómo se puede aplicar el método a enunciados compuestos con varias conectivas diferentes.
La finalidad del método es comprobar si un enunciado es tautológico, contradictorio o ninguna de las dos cosas. Por lo tanto, lo que queremos hacer es simplemente estudiar todas las combinaciones posibles de valores de verdad de los enunciados simples y analizar después la tabla de verdad que resulta para la expresión compuesta. En el caso de p Ú ~ p hay dos posibilidades: o p es verdadero o p es falso. Sí p es verdadero su negación es falsa y a la inversa.
Una disyunción de p y su negación ha de ser siempre verdadera, pues en cualquier caso uno de los dos elementos de la disyunción es verdadero. Si lo escribimos en forma de tabla de verdad, tenemos
(1) p ~p pÚ ~p
t f t
f t t
(1) puede también escribirse en la forma (1’)
(1’) p ~ p
t t f t
f t t f
Si se tratara de dos variables, tendríamos cuatro posibilidades, si fueran tres las variables, habría ocho posibilidades (y, en general, hay 2n posibilidades, siendo n el número de variables de enunciados distintas y 2, la base, el número de valores de verdad).
Estudiemos dos ejemplos más.
(2) (p & q) ®p
p q p&q p (p & q) ®p
t t t t t
t f f t t
f t f f t
f f f f t
Sean cuales sean los valores de verdad que damos a los enunciados simples, tenemos un enunciado verdadero. Por lo tanto, (2) es una tautología
(3) (p & q) ® (p Ú r)
| p | q | r | p&q | pÚr | (p &q) ® (p Ú r) |
| t | t | t | t | t | t |
| t | t | f | t | t | t |
| t | f | t | f | t | t |
| t | f | f | f | t | t |
| p | q | r | p&q | pÚr | (p &q) ® (p Ú r) |
| f | t | t | f | t | t |
| f | t | f | f | f | t |
| f | f | t | f | t | t |
| f | f | f | f | f | t |
De nuevo se trata de una tautología, puesto que para todas las combinaciones posibles de valores de verdad de los constituyentes el valor de la expresión compleja es t.
No todos los enunciados en lógica proposicional son, sin embargo, tautologías.
(4) ~p ® (p Ú r)
| p | q | ~p | pÚq | ~p ® pÚq |
| t | t | f | t | t |
| t | f | f | t | t |
| f | t | t | t | t |
| f | f | t | f | t |
(4) no es tautología ni contradicción sino lo que antes hemos llamado un enunciado sintético: un enunciado cuyo valor de verdad depende de cómo sea el mundo. La propiedad característica de un enunciado sintético de t y f en la columna final bajo la conectiva principal de la expresión. Esto significa que el valor de verdad del enunciado compuesto depende de los valores de verdad de los enunciados constituyentes; y el valor de verdad de los enunciados simples depende, naturalmente, de cómo sea el mundo. Esta es la razón de que digamos 4ue los enunciados que no son ni tautologías ni contradicciones, son enunciados sintéticos, es ‑decir, enunciados cuyos valores de verdad están determinados por la configuración del mundo.
(5) ~(p ® (p Ú r))
p q p Ú q p® (p Ú q) ~(p ® (p Ú r))
t t t t f
t f t t f
f t t t f
f f f t f
(5) es una contradicción. Todas las combinaciones posibles de valores de verdad dan el valor final f.
Las contradicciones de] mismo tipo que (5) aclaran la relación entre contradicciones y tautologías. p ® (p Ú r) es, como se puede comprobar, una tautología, mientras que ~(p ® (p Ú r)) es una contradicción. Negando una tautología surge una contradicción, al igual que si negamos una contradicción, obtenemos una tautología.
La forma lógica de un enunciado, que en lógica de enunciados está determinada por las propiedades veritativo‑funcionales de las conectivas, puede compararse con una máquina en la que si se introducen los valores de verdad de los enunciados simples, el producto son los valores de verdad del enunciado compuesto. Si la máquina da siempre t, independientemente del valor de verdad sobre el que ha operado, estamos ante una tautología.
Este operar mecánico de la forma lógica es consecuencia del hecho de que cada conectiva lógica relaciona de manera precisa cada posible combinación de valores de verdad con el valor de verdad del enunciado compuesto. Las relaciones estructurales entre enunciados que se estudian en lógica proposicional pueden, por lo tanto, entenderse como relaciones entre enunciados respecto de su valor de verdad. La función de una conectiva lógica es decidir, para cada combinación posible de valores de verdad, cual es el valor de verdad resultante para esa combinación. El valor de verdad de un enunciado compuesto queda unívocamente determinado por la conectiva lógica y las combinaciones posibles de valores de verdad de los enunciados simples.
Por lo tanto, es natural decir que las conectivas designan funciones que proyectan uno o varios valores de verdad en un valor de verdad y sólo en uno. Llamamos funciones de verdad a estas funciones.
Salvo en (3) hemos escogido siempre nuestros ejemplos de cálculo de los valores de verdad de tal modo que tuviéramos que manejar sólo dos variables. La razón es que el número de combinaciones posibles de valores de verdad crece exponencialmente con el número de variables de enunciado distintas; los cálculos se hacen entonces, en el mejor de los casos, aburridos. En expresiones con más de dos variables tenderemos, debido a ello, a usar el llamado razonamiento indirecto (llamado también, a menudo, reductio ad absurdum).
Para hacer un razonamiento indirecto procedemos como sigue. Suponemos que la expresión que nos interesa es falsa. Si este supuesto no conduce a una contradicción, sabemos que la expresión no es una tautología. La razón es que una tautología es siempre verdadera. Si es de alguna manera posible que la expresión que nos interesa sea falsa, la expresión no puede ser tautológica. Sin embargo, si nuestro supuesto de que la expresión es falsa conduce a una contradicción (es decir, no es posible que la expresión sea falsa), tenemos una tautología.
Una vez que hemos mostrado que el suponer que un cierto enunciado es falso no conduce a contradicciones, todavía queda por determinar si el enunciado es una contradicción o un enunciado sintético. Este problema suele quedarse sin resolver, puesto que, en lógica, lo que nos interesa primordialmente es saber si una expresión es una tautología o no. Si estamos interesados en el problema de determinar si un enunciado es una contradicción, invertimos simplemente el proceso de razonamiento: suponemos que el enunciado es verdadero y comprobamos si este supuesto lleva a una contradicción.
Veamos algunos ejemplos de razonamiento indirecto.
(6) Nivel ((p Ú q) & r) ® p
(1) f
(2) t f
(3) t t
(4) f t
En el nivel (1) suponemos que el valor de verdad de la expresión entera es f. La tabla de verdad de la implicación material nos dice que una implicación sólo puede ser falsa cuando su antecedente es verdadero y su consecuente falso, que es lo que se indica en el nivel (2). Las dos t en el nivel (3) son necesarias, según la tabla de verdad, para que la conjunción pueda tener el valor verdad t que se le ha atribuido en el nivel (2). Una conjunción es verdadera sólo si los dos enunciados que la forman lo son. El nivel (4) está determinado por el hecho de que antes hayamos asignado f a p: una variable tiene siempre el mismo valor de verdad en cada asignación. Podemos, entonces, hacer uso del hecho de que la disyunción en el nivel (3) tiene el valor t. Según las condiciones de verdad de la disyunción, q ha de tener el valor t. Dado que no hemos llegado a una contradicción por suponer que (6) era falso, (6) no puede ser una tautología.
(7) Nivel (((~ p ® ~ (q Ú r)) & (s ® r)) & s) ® p
(2) f
(3) t f
(4) t t
(5) t f1 t f t 2 t*
(6) f f* Contradicción
Los valores asignados a p y s en el nivel (5) (marcados con los índices (1) y (2) respectivamente) son los que atribuyeron a estas variables en los niveles (2) y (5) respectivamente.
En este ejemplo dejamos que el lector mismo haga el razonamiento, inspirándose en su conocimiento de las propiedades veritativo‑funcionales de las conectivas. Sólo diremos que, como es claro, en el ejemplo (7) termina apareciendo una contradicción (véanse las variables marcadas con *). Nos vemos obligados a suponer que r es falso y verdadero a la vez. Debido a esta contradicción hemos de admitir que (7) no puede ser falso. Por lo tanto es una tautología.
¿Cómo podemos operar con enunciados cuyas conectivas principales no son implicaciones? Si suponemos, por ejemplo, que una conjunción es falsa, hay que estudiar tres posibilidades. El método heroico consiste en analizar cada una de las posibilidades en el modo indicado más arriba. Existe, sin embargo, otra posibilidad. Podemos usar nuestro conocimiento de las equivalencias lógicas para transformar en implicaciones expresiones cuya conectiva principal no es una implicación. A continuación damos una lista de leyes lógicas muy conocidas, algunas de las cuales pueden usarse para pasar de una expresión lógica a una implicación equivalente, haciendo así más fácil la reducción al absurdo.
(8) (i) p Ú ~ p
(ii) ~ (p & ~ p)
(iii) p º p
(iv) (p Ú q) º ~ (~ p & ~ q)
(v) (p & q) º ~ (~ p Ú ~ q)
(vi) ~ (p Ú q) º (~ p & ~ q)
(vii) ~ (p & q) º (~ p Ú ~ q)
(viii) (p®q) º ~(p & ~q)
(ix) (p & q) º ~(p®~q)
(x) (p ® q) º (p & ~ q)
(xi) (p & q) º (p ® ~ q)
(xii) (p v q) º (~ p ® q)
(xiii) (p ® q) º (~ p v q)
(xiv) ~ ~ p º p
(xv) p º p v p
Por medio de estas tautologías y equivalencias u otras similares’ puede el lector modificar con facilidad una expresión de modo que adquiera una forma más fácil de manejar. Considérese
(9) ~ (((p & (q v ~ q)) ®p) & ~ p)
(9) tiene un aspecto realmente complicado, así que la transformamos en (10) usando (8) (xi).
(10) ((p & (q v ~ q)) ® p) ® ~ ~p
Finalmente tenemos una implicación sobre la que podemos intentar un razonamiento indirecto. Si transformamos (10) en (11).
(11) ((p & (q v ~ q)) ® p) ® p
f f t t f t t f f f
y hacemos una reductio ad absurdum, vemos que (9) no es una tautología.
EJERCICIOS
1. ¿Cuál de los tres enunciados siguientes no puede formalizarse en lógica de enunciados del mismo modo que los otros dos? ¿Por qué?
(a) Luis y Ricardo son comuneros
(b) Luis y Ricardo son parientes
(c) A Luis y Ricardo les gusta beber
2. Inténtese representar los siguientes enunciados con variables de enunciado y conectivas lógicas.
(a) Si esto es verano, que venga Dios y lo vea
(b) Los limones son bonitos pero amargan
(c) Puedes si quieres
(d) Vendrá hoy o mañana, pero no más tarde
(e) Si no existen ni Dios ni el demonio, es difícil ser religioso
(f) Echa al gato o me voy
3. Indique los valores de verdad de las siguientes expresiones compuestas partiendo del supuesto de que p y q son verdaderos y r es falso.
(a) ~ p
(b) ~ (p & r)
(c) ~ (p v q)
(d) p v (q & r)
(e) r ® ((q & r) v (p v q))
(f) r º (p & r)
4. ¿Qué expresiones, entre las siguientes, son tautologías?
(a) ~ (p & ~ p)
(b) (p v q) ® p
(c) ~ (p&q) º ~‑p v ~ q
(d) ~ ((p º q) º (p º ~ q))
(e) (p ® ~ q) v (q ® ~ p)
(f) ((p º q) º p) º q)
(g) (p & q) v (p º ~ q)
(h) (p v (q & r)) º ((p v q) & (p v r))
5. ¿Puede considerarse función de verdad la conectiva porque? Razónese la respuesta.
8. Determinar, por razonamiento indirecto, si las siguientes ex presiones son tautologías.
(a) p ® (q ® (r ® (s ® (t ® p))))
(b) ((º q) & (q º r)) ® (p º r)
(c) (p & (q º r)) ® ((p & q) º r)