Allwood, J.; Andersson, L. Y Dahl, Ö. (1981): Lógica para Lingüistas. Madrid: Paraninfo. Pp. 70-108
Lógica de Predicados
Pulse aquí para revisar el listado de SÍMBOLOS
Hemos visto, en el capítulo de lógica de enunciados, que se puede decidir si una inferencia es correcta o un enunciado verdadero (tautológico) por medio del uso de técnicas como la de las tablas de verdad.
Hay sin embargo muchas inferencias en el lenguaje natural que intuitivamente son correctas, pero cuya corrección no puede justificarse en el marco de la lógica de enunciados, por ejemplo (1).
(1) Si todos los, alces son listos y Bruce es un alce, entonces Bruce es listo
Todo el mundo aceptaría como correcto un razonamiento de este tipo y sin embargo su validez no puede justificarse en lógica de enunciados. (1) se analizaría en lógica proposicional como (p & q) ® r, expresión que es cualquier cosa menos tautológica como se ve por su tabla de verdad. Por el contrario, la lógica de predicados nos ofrece un instrumento con el que podemos mostrar que el razonamiento (1) es lógicamente correcto. Podemos decir, de un modo general, que la lógica de predicados nos lleva de las relaciones lógicas entre enunciados a las relaciones lógicas que se dan en el interior de los enunciados.
Examinemos ahora con más detalle cómo podemos mostrar la validez de (1). Empecemos con un enunciado simple.
(2) Bruce es un alce
Este enunciado dice algo acerca de un individuo. El individuo es Bruce y se dice de él que tiene la propiedad de ser un alce. Este tipo de enunciado se llama enunciado predicativo (se predica algo, por ejemplo una propiedad, de un individuo).
Las correspondientes estructuras lingüísticas, sintagma nominal y sintagma verbal, pueden ayudarnos en cierta medida a desarrollar las intuiciones pertinentes en este contexto.
Los siguientes enunciados tienen la misma forma lógica que (2), puesto que predican algo de un individuo.
(3) El oso está dormido
El Rey Canuto se rindió
Olaf era un vikingo
El Este es rojo
Simbolizamos los sujetos en los enunciados anteriores por medio de a, b, c, d... Estos símbolos se llaman constantes de individuo (letras latinas minúsculas). Los predicados de los enunciados los simbolizamos con A, B, C, D... Estos símbolos se llaman constantes de predicado o simplemente predicados (letras latinas mayúsculas).
Ahora podemos simbolizar (2) en lógica de predicados. Por mor de la brevedad, atribuimos la letra b a Bruce y la letra M a la propiedad de ser un alce. El enunciado se presenta como sigue. Téngase en cuenta que, por convención, el predicado se coloca al principio de la expresión.
(4) M(b)
En (4) hablamos de un cierto individuo, Bruce, y de: una cierta propiedad, la de ser un alce, y decimos que Bruce tiene la propiedad de ser un alce. Podemos también formar la siguiente expresión.
(5) M(x)
En (5) x no es una constante de individuo sino una variable de individuo. Esto significa que x no está en lugar de un individuo concreto sino de un individuo cualquiera (o, dicho de otro, en lugar de un individuo arbitrariamente elegido). Tal como está escrito, (5) no expresa ninguna proposición. Esta es la razón de que (5) no sea considerado, en lógica, como enunciado sino como enunciado abierto.
Podemos dar un paso más en la escala de abstracción y formar la siguiente, expresión.
(6) F(x)
En esta fórmula tenemos no sólo una variable de individuo sino también una variable de predicado, F (la mayúscula griega phi). Una variable de predicado nos remite no a una propiedad concreta sino a una propiedad cualquiera (una propiedad indeterminada).
Tal como está escrita, (6) puede considerarse una expresión sin sentido. Indica la posibilidad de predicar una propiedad cualquiera de un individuo cualquiera. No se hace ninguna afirmación de existencia. Sin embargo, como veremos luego, las expresiones del tipo de (6) pueden utilizarse en lógica para ciertos fines.
Constantes y variables de individuos se suelen agrupar bajo el nombre común de términos de individuo. Del mismo modo, variables y constantes de predicado se agrupan bajo el nombre de términos de predicado.
Se puede decir que los enunciados que aparecen en (2) y (3) tienen la misma estructura o forma lógica. Están formados por un término de predicado seguido de un término de individuo. Tienen, por lo tanto, la forma lógica representada en (7).
(7) P(t)
Ni que decir tiene que no todos los enunciados tienen la forma lógica de (7). Los siguientes enunciados, por ejemplo, tienen otra forma lógica.
(8) Thor robó el martillo
Wotan admira a Thor
Dios creó el mundo
Wotan es más sabio que Dios
En estos enunciados aparecen predicados con dos argumentos. Argumento es un término que se emplea para referirse, entre otras cosas, a lo que en gramática se llama sujeto u objeto. Los términos de individuo que siguen al predicado en una expresión de la lógica de predicados se llaman argumentos del predicado. Si un predicado lleva un sólo argumento, se llama unario; si dos, binario; si tres, ternario, etc. Ejemplificamos esta terminología en (9).
(9) P(t) predicado unario (o monádico)
P(t1, t2) predicado binario (o diádico)
P(t1, t2, t3) predicado ternario
P(t1, t2, t3, t4) predicado cuatemario
P(t1, t2, ..., tn) predicado n‑ario
Dado que los predicados en (8), robó, admira, creó y es más sabio que, llevan cada uno dos argumentos, son predicados binarios. Los enunciados en (8) tienen, por lo tanto, la forma lógica P(t1, t2). Los enunciados de (10) pueden formalizarse como P(t1, t2, t3)es decir, contienen predicados ternarios. Los argumentos están subrayados.
(10) Juan le dio a Juana la manzana
EL guía mostró Gothenburp al turista
Wotan ofreció cerveza a Thor
No es fácil encontrar enunciados en el lenguaje natural que tengan predicados con más de tres argumentos sin entrar en cuestiones controvertidas. El siguiente enunciado podría considerarse, sin embargo, como un ejemplo de uso de un predicado con cuatro argumentos.
(11) Juan le compró a Juana un reloj por cinco libras esterlinas
En los anteriores enunciados vemos que los predicados en las fórmulas lógicas corresponden con bastante exactitud a los predicados del análisis gramatical. Para un lógico es, sin embargo, una cuestión sin mayor interés la de si un predicado lógico corresponde a una palabra o expresión simple en el lenguaje natural. Desde el punto de vista lógico expresiones muy complejas como toma el aperitivo los domingos por la manaña entre 11 y 12 o es un lingüista de pelos largos que se interesa por la relación entre la lógica modal y la dialectología pueden considerarse predicados en una fórmula lógica. Esto implica que un enunciado como Thor robó el martillo no tiene necesariamente que analizarse como F(a, b), es decir, como un predicado binario, sino que puede analizarse también, en principio, como F(a), con un predicado unario, interpretando F como el predicado robó el martillo, aunque el primer tipo de análisis sea el más natural desde un punto de vista lingüístico.
2. CUANTORES
Volvamos a la primera parte del primer ejemplo de este capítulo.
(1) Todos los alces son listos
Si analizáramos este enunciado del mismo modo que los otros enunciados del capítulo tendríamos
(2) C (todos los alces)
del mismo modo que
(3) C (Bruce)
En el caso de (2) el problema es que no podemos sustituir la expresión todos los alces por una constante de individuo. Todos los alces no se refiere a un individuo y en cambio el nombre Bruce, sí. Lo que afirma (2) en realidad es que si encontramos un alce, podemos esperar que sea listo. Dicho de otro modo: escoja un alce cualquiera y encontrará que es listo.
Introducimos un nuevo tipo de constante lógica con el fin de analizar enunciados del mismo tipo que (1): el cuantor universal, con el significado ‘todo(s)’ ‘cada’ o ‘para todo(s) vale que’. El cuantor universal se representa por el símbolo ". Un enunciado como el de Heráclito ‘todo fluye’ se formaliza de la siguiente manera por medio del cuantor universal.
(4) "x F(x)
(4) se puede leer como ‘Para todo x, x fluye’. De modo similar, (1) se puede analizar por medio de (5).
(5) "x (M(x) ® C(x))
Esta expresión puede leerse de cualquiera de los modos siguientes:
| (6) |
(a) Para todo x, si x es un alce, entonces x es listo (b) Vale decir de todo objeto que si es un alce, entonces es listo (e) Si algo es un alce, entonces es listo (d) Todos los alces son listos |
Para entender la función de fórmulas como (5), es importante saber qué es una variable. La x en "x está por cualquier individuo en el universo del discurso. Es una variable que se refiere a los objetos e individuos del universo: su rango está constituido por todos los objetos e individuos del universo.
El rango no necesita estar constituido por todos los objetos del universo en que vivimos, aunque este sea el caso en el ejemplo anterior. En un libro de matemáticas el rango puede ser el conjunto de los números y en un libro de sociología, el conjunto de los seres humanos, etc. En este contexto se usa el concepto de universo del discurso, es decir, todos los objetos de que se habla en un cierto contexto. Este concepto se introdujo en el capítulo 2.
Para lograr una mejor comprensión de la diferencia entre enunciados simples como F(b) (Bruce fluye) y enunciados cuantificados como, "x F(x), volvemos al concepto de enunciado abierto. Un enunciado abierto es una expresión de la forma (7)
(7) F(x) (léase ‘x fluye’)
Dado que x es una variable que no se refiere a ningún individuo en concreto, no podemos decir con sentido que F(x) exprese una proposición o que haga una afirmación. No se puede decir que un enunciado abierto es verdadero o falso. Un enunciado simple como Bruce fluye, por el contrario, es siempre verdadero o falso, tiene un valor de verdad. ¿Cómo podría contestarse a la pregunta de si x fluye? La única respuesta posible sería ‘depende de qué o quién sea x’. Si x se refiere al Támesis, entonces es verdad, pero si x se refiere al Rey Canuto, probablemente es falso que x fluya. Decir que el Rey Canuto no satisface el enunciado abierto F(x) es equivalente a decir que F(c), en donde c se refiere al Rey Canuto, es enunciado falso.
Un modo de construir un enunciado partiendo de un enunciado abierto es asignar un cierto valor a la variable. Como hemos indicado más arriba, el modo de hacerlo es sustituir la variable en la expresión por una constante de individuo. Los enunciados abiertos se llaman también funciones enunciativas. Entendemos a qué se alude con este término si pensamos el enunciado abierto como una función que toma individuos como argumentos y diferentes enunciados como valores de verdad. Otro modo de crear un enunciado, partiendo de un enunciado abierto, es colocar un cuantor seguido de una variable al principio del enunciado abierto. Por este método, partiendo de (7), conseguimos el enunciado del principio.
(8) "xF(x) ‘Todo fluye’
(8) afirma que todos los objetos en el universo del discurso satisfacen la función enunciativa F(x). Esto es obvio. Si hubiera un objeto en el universo del discurso, pongamos a, que no, satisfaciera la función enunciativa, el enunciado ‘Todo fluye’ sería falso. Por lo tanto, si F(a) es un enunciado falso, el enunciado "xF(x) es también falso, dado que a es un elemento del rango de x (es decir, dado que a pertenece al universo del discurso).
Es importante tener en cuenta que se cuantifican enunciados abiertos y no enunciados. Cuantificar enunciados produce extraños resultados.
(9) "x F(b)
(9) se leería como sigue ‘Para todo x, Bruce fluye’, expresión que, claramente, no tiene sentido.
Los enunciados abiertos pueden presentar estructuras más compleja que la de los enunciados predicativos simples. Así en (10), por ejemplo.
(10) M(x) ® C(x) ‘Si x es un alce, entonces x es listo’
Si partimos de (10), le ponemos paréntesis y un cuantificador delante, conseguimos un enunciado.
(11) "x (M(x) ® C(x))
Hay que tener en cuenta que aunque podemos escoger cualquier individuo como valor de la variable x, hay que mantener ese mismo individuo como valor de x en las dos expresiones M(x) y C(x), cuando aparecen dentro de los mismos paréntesis, como es el caso en (11). Decimos que el cuantor liga las equis en M(x) y C(x).
El alcance de cuantor es la expresión dentro de los paréntesis que le sigue inmediatamente.
Una variable ligada por un cuantor es una variable ligada. Las variables que no están ligadas se llaman variables libres, como ocurre con la última aparición de x en (12), por ejemplo.
(12) "x (F(x) ® L(x) & K(x)))
En (13), por el contrario, la variable correspondiente está ligada
(13) "x(Fx) ® (L(x) & K(x)))
Esto significa que el valor de x en K(x) en (12) es independiente del valor de las equis que aparecen dentro de los paréntesis. Este no, es, sin embargo, el caso para la segunda expresión. En (12), K(x) se puede sustituir por K(y) sin cambiar el significado de la expresión. En (13) no se puede hacer una sustitución similar. Las expresiones lógicas que contienen variables libres no constituyen enunciados sino enunciados abiertos.
Dentro del alcance de un cuantor cada una de las variables está siempre por un único individuo.
En (14) aparecen una serie de expresiones lógicas en las que el alcance de cada cuantor está subrayado. No nos interesa aquí que significan esas expresiones ni a qué se refieren los predicados. El fin de las expresiones es familiarizar al lector con los conceptos de ‘alcance’, ‘variable ligada’, ‘variable libre’ y ‘enunciado abierto’.
(14) (a) F(a) Ú "x (K(x) ® G(x, a))& "x (G(x, a))
(b) "x (K(x) ® F(y) & G(x, a))
(c) "y "x (K(x) ® (F(y) & G(x, a))
(d) "x ((K(x) & F(a)) ® "y (G(x, y) Ú G(y, y) & "z (F(z) ® G(z, y)))
(14) (a) no es un enunciado abierto, puesto que no aparece en él ninguna variable libre. (14) (b) es un enunciado abierto, dado que contiene una variable libre, a saber, la y de F(y). (14) (e) es un enunciado con dos cuantores cuyo alcance se superpone. (14) (d) muestra una expresión con tres cuantores. El alcance de dos de ellos está dentro del alcance del primero. (14) (d) no es un enunciado sino un enunciado abierto, puesto que la última variable de la expresión no está ligada por ninguno de los cuantores.
En castellano se pueden formar una infinidad de enunciados que no contienen el cuantor todo (cada) sino, otra palabra que opera como un cuantor: uno, dos, tres, algunos, ninguno, varios, muchos y pocas. Todos los elementos de la categoría gramatical de los pronombres indefinidos se pueden considerar, en cierto modo, como cuantores.
En lógica, normalmente, basta con aceptar dos cuantores. Estos dos cuantores tienen las dos características siguientes. Son importantes para la formalización de las matemáticas y sus propiedades lógicas son relativamente simples. El primero de ellos es el cuantor universal, que hemos estudiado más arriba.
El segundo es el llamado cuantor existencial. Se escribe $ y significa, grosso modo, ‘algo/alguien’ o ‘hay algo/alguien’. Los siguientes ejemplos muestran cómo se usa este cuantor.
(15) (a) Alguien es conservador $x C(x)
(b) Existe un unicornio $x U(x)
(c) Hay alguna chica más simpática que Pepa $x (G(x) & S(x, a))
donde C está por ‘conservador’
U ‘ser un unicornio’
S ‘ser más simpático que’
G ‘ser una chica’
a Pepa
(15) muestra cómo es posible representar por el cuantor universal expresiones castellanas bastante diferentes. La mejor manera de leer $x en una expresión lógica es ‘Hay un x tal que...’ o, para ser más precisos, ‘Hay por lo menos un x tal que...’. El cuantor existencial indica que al menos un objeto del universo del discurso satisface el enunciado abierto que sigue al cuantor.
Las expresiones lógicas en (15) se leerían del modo siguiente.
(16) (a) Hay al menos un x tal que x es conservador
(b) Hay al menos un x tal que x es un unicornio
(c) Hay al menos un x tal que x es una chica y x es más simpático que Pepa
Enunciados como los de (16) son ‘traducciones inversas’, símbolo a símbolo, de las expresiones en (15) al castellano y por ello suenan más bien torponas.
Los cuantores universal y existencial funcionan, en ciertos aspectos, de manera diferente. Una de las cosas que le parecen extrañas al que comienza a estudiar lógica es el modo en que se representan los dos enunciados castellanos siguientes:
(17) Todas las mozas son guapas "x (M(x) ® P(x))
(18) Alguna moza es guapa $x (M(x) & P(x))
La única diferencia entre (17) y (18) parece consistir en que contienen cuantores diferentes. Si miramos, en cambio, las representaciones lógicas de estos enunciados, vemos que no sólo tienen diferentes cuantores sino que también contienen conectivas lógicas diferentes. Al principio esto puede parecer extraño, pero es fácil mostrar que sería imposible cambiar las conectivas lógicas en (17) y (18).
La representación lógica de (17) contiene una implicación. Si se cambia la implicación por una conjunción, tenemos (19).
(19) "x (M(x) ® P(x))
(19) afirma que todo individuo en el universo del discurso es una moza y es guapa. Así pues, (17) y (19) no son equivalentes. (17) no, excluye la posibilidad de que existan algunos mozos feos en el universo del discurso, como lo hace (19). Esto significa que (19) no es una representación correcta del significado del enunciado (17).
(18) contiene una conjunción. Si se cambia la conjunción por una implicación, tenemos (20).
(20) $x (M(x) & P(x))
(20) afirma que hay al menos un x en el universo del discurso tal que si x fuera una moza, entonces x sería guapa. (20) es verdadero si hay algún objeto en el universo del discurso que no sea una moza (esto se debe a la definición de la implicación material en lógica). (18) no es verdadero en tales circunstancias. Además (20) no implica que existan mozas en el universo del discurso, mientras que (18), sí. Es claro, entonces, que (18) y (20) no son equivalentes y que (20) es una representación incorrecta del significado de (18).
Desde un punto de vista lingüístico, tanto la representación lógica de (17) como la de (18) no parecen totalmente intuitivas. (21) y (22) son representaciones lógicas de (17) y (18) más satisfactorias lingüísticamente.
(21) "x P(x) ‘para toda moza x, x es guapa’
x Î M
(22) $x P(x) ‘para alguna moza x, x es guapa’
x Î M
En estas expresiones hemos usado lo que habitualmente se llama cuantificación restringida. La expresión que está debajo del cuantor indica el rango de la cuantificación, en este caso, el conjunto de las mozas. M está por el conjunto de las mozas y e es la relación ‘elemento de’ de la teoría de conjuntos. (21) y (22) ponen de manifiesto el paralelismo entre los dos enunciados, cosa que no ocurre en las representaciones lógicas de (17) y (18). La única diferencia entre (21) y (22) estriba en la elección del cuantor. Escribiendo el rango de la cuantificación como un suscrito evitamos usar conectivas diferentes en el interior de las expresiones. La cuantificación restringida no se usa habitualmente en lógica, pero se puede incluir a fin de lograr un análisis más adecuado del lenguaje natural.
En una expresión lógica puede haber más de un cuantificador. Así, por ejemplo, (23) es una expresión bien formada de la lógica de predicados.
(23) "x $y "z R (x, y, z)
Cuando hay más de un cuantor delante de un enunciado, abierto, el orden en que están escritos no es arbitrario, puesto que es ese orden lo que indica el alcance de cada uno respecto de los demás.
Comparemos las dos expresiones siguientes, en donde F(x, y) está por ‘x es el padre de y’.
(24) "x $y F(x, y) ‘para todo y, hay un x tal que x es el padre de y’
(25) "x $y F(x, y) ‘hay un x, tal que, para todo y, x es el padre de y’
La única diferencia entre estos dos enunciados es que el cuantor existencial está dentro del alcance del cuantor universal en (24), mientras que en (25) ocurre al revés. Esto influye de manera considerable en el significado de los enunciados. En castellano ortodoxo, (24) significa ‘Todo el mundo tiene padre’, cosa que parece razonable. (25), en cambio, significa ‘Alguien es padre de todo el mundo’, lo que ya no parece tan razonable.
En (24) se dice que sea cual sea el individuo que consideramos, es siempre posible encontrar algún individuo que es su padre. En (25) se afirma que hay un individuo tal que, dado un individuo cualquiera, el primero es el padre del segundo. Esto puede sonar un poco enrevesado, pero ahora veremos un modo de aclarar estas diferencias.
Hay enunciados en castellano, como ‘todo el mundo admira a alguien’, que son ambiguos precisamente en dependencia del alcance del cuantor. Los diferentes sentidos de estos enunciados corresponden a expresiones diferentes en la lógica de predicados. El enunciado que hemos mencionado antes tiene dos lecturas. A está por ‘admira’ en las expresiones que siguen.
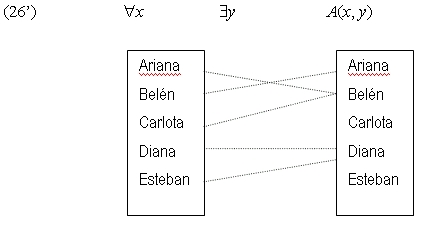
(26) "x $y A(x, y) ‘todo el mundo tiene alguien a quien admira’
(27) $y "x A(x, y) ‘hay alguien a quien todo el mundo admira’
Para ver cómo funciona el alcance del cuantor vamos a considerar un universo del discurso pequeño, pongamos, cinco individuos. Supongamos que el universo del discurso contiene los individuos Ariana, Belén, Carlota, Diana, Esteban. El rango de los cuantores es el conjunto de estos cinco individuos.
Estudiaremos primero (26). Debajo de los cuantores ponemos el rango de las variables. Las líneas de puntos indican que el primer individuo admira al segundo.

(26) dice que es posible encontrar, para cada individuo, del primer conjunto, un individuo en el segundo conjunto tal que el primero admira al segundo. Esto es lo que indican las líneas en (26’). Cada uno de los individuos en el universo del discurso admira a alguien del universo del discurso.
(27) ha de entenderse de diferente manera. Este enunciado dice que es posible encontrar a alguien en el universo del discurso que es admirado por todos, tal como se pone de manifiesto en 27’).
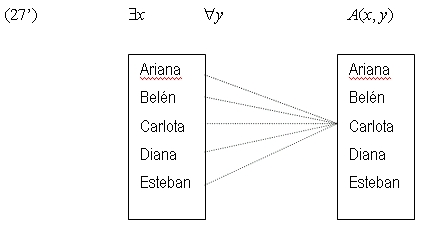
Ahora se ven con claridad las diferencias entre (26) y (27). Lo importante de (26’) es que encontramos que, para cada individuo en el primer conjunto, hay un individuo en el segundo al que aquél admira. Los individuos en el primer conjunto pueden admirar a individuos diferentes en el segundo conjunto, pero cada uno de ellos ha de admirar a alguien en el segundo conjunto. Lo importante de (27) es que todos los individuos del primer conjunto admiran al mismo individuo en el segundo. Como se ve en (27) todos admiran a Carlota.
Todavía hay que apuntar una cosa más. (27) seguiría siendo verdadero si, por ejemplo, Ariana admirara a Belén además de admirar a Carlota. Lo que importa es que todos admiren a Carlota.
El enunciado (27) implica el enunciado (26), pero, (26) no implica (27). Esto se ve a partir del esquema anterior. Si todo el mundo admira al mismo individuo, ha de ser verdad que todo el mundo admira a alguien.
En otras palabras,
"x $y F(x, y) ® "x $y F(x, y)
pero no
"x $y F(x, y) ® $x "y F(x, y)
Las ambigüedades de alcance que se producen en enunciados que contienen dos cuantores son interesantes lingüísticamente. A menudo, sucede que la entonación cambia un enunciado potencialmente ambiguo en uno que no lo es. Un ejemplo de este fenómeno es el siguiente verso de una canción que fue popular hace algunos años: Everybody loves samebobody sometime (Todo el mundo ama a alguien alguna vez). Si se conoce la canción, se estará de acuerdo en que el enunciado sólo se puede entender de tal modo que el cuantor universal tenga el alcance más amplio.
Otro rasgo de los cuantores que ha sido ampliamente discutido por los lingüistas es el siguiente. El orden de los cuantores en un enunciado castellano corresponde a menudo al orden que damos a los cuantificadores en la representación lógica del significado de ese enunciado. Comparemos los enunciados siguientes.
(28) (a) Todos los que están en esta habitación hablan dos idiomas.
(b) Hay dos idiomas que son hablados por todos los que están en esta habitación.
(28) (a) favorece claramente una lectura en la que el cuantor universal tenga el alcance más amplio. (28) (b), por el contrario, inclina a la lectura en la que la expresión ‘hay dos lenguajes’ tiene más amplio alcance. Puede ser que ambas expresiones sean ambiguas, pero, es claro que, en cada caso, se prefiere la lectura cuya representación lógica presenta los cuantores en el mismo orden que en castellano. Dado que la transformación pasiva, que se usa para relacionar (28) (a) con (28) (b), se entiende como, transformación que no afecta al significado, los pares de enunciados del mismo tipo que (28) presentan un problema para el lingüista. Pares de enunciados como los de (.28) se mencionan ya en Chomsky (1957).
Un problema similar lo crean pares de enunciados como los siguientes.
(29) (a) Alguien no explicó la situación
(b) La situación no fue explicada por alguien
Lo relevante aquí no es el orden de los cuantores sino la posición de la negación con respecto a los cuantores. Para muchos hispano‑hablantes (29) (b) es ambiguo y tiene las dos lecturas siguientes, entendiendo E por ‘explicar’ y ‘s’ por situación.
(30) (a) ~$x E(x, s) ‘no hay un x tal que x explicara s’
(b) $x~ E(x, s) ‘hay algún x tal que x no explicó s’
(30) (a) dice que nadie explicó la situación. (30) (b) dice que no todo el mundo explicó la situación: alguien lo hizo y alguien, no. (29) (b) puede entenderse de las dos maneras, pero (29) (a) probablemente sólo puede entenderse en el sentido de (30) (b). Y sin embargo, (29) (b) se relaciona con (29) (a) por medio de la transformación pasiva.
Abandonamos por el momento las ambigüedades del alcance del cuantificador con estos ejemplos, aunque encontraremos de nuevo, ocasión de tratarlas en el capítulo de lógica modal.
EJERCICIOS
1. Sean a= Alicia A= admirar
b= Bartolo D= desdeñar
f= Francisco
Traducir las siguientes expresiones de la lógica de predicados al castellano
(a) A(b, f)
(b) A(b, f) & D(f, b)
(c) $ xA(x, x)
(d) ~"x D(x, f)
(e) "x(A(x, j) ® D(x, x))
(f) ~ $x "yA(y, x)
(g) "x "y(A(x, y) ® ~D(x, y))
2. Formalizar los siguientes enunciados en lógica de predicados
(a) Canuto es Danés
(b) Canuto era liberal pero Olaf era socialista
(c) Luisa no le gusta a ningún chico
(d) Todos los estudiantes leen algún libro
(e) Ningún estudiante contesta todas las
(f) Si todos los estudiantes catean, ninguno se sentirá feliz
(g) Se puede, si se intenta
3. Clasifíquense las siguientes relaciones según la reflexividad, simetría y transitividad.
(a) ‘ganar tanto dinero como’
(b) ‘ganar tanto o más dinero que’
(c) ‘ser el abuelo de’
(d) ‘enamorarse de’
(e) ‘ser el hermano de’
(4) ¿Es una función la relación entre una persona y sus huellas digitales?
(5) Dar ejemplos de
(a) una relación multívoca
(b) una relación unívoca a la derecha
(c) una relación unívoca a la izquierda
(d) una relación biunívoca
(6) Dar un ejemplo de un enunciado en lógica de predicados que sea falso en todo mundo posible.
7. Traducir los dos enunciados siguientes a la lógica de predicados.
(a) Ricardo vio un oso y Juan también lo vio.
(b) Ricardo vio un oso y Juan también vio uno.
(8) Formalizar la ambigüedad del siguiente enunciado por medio de la lógica de predicados.
Todo el mundo odia a alguien
9. Dar dos expresiones castellanas tal que una sea la conversa de la otra.
10. ¿Cómo se interpreta extensionalmente un predicado en lógica de predicado?
11. Formalizar en lógica de predicados el siguiente enunciado:
Existe un poder maligno
12. ¿Qué es un enunciado abierto?
13. ¿Cuál de los siguientes enunciados es equivalente?
(a) "x(F(x) ® G(x))
(b) "x(F(x) & G(x))
(c) ~ $x(F(x) & ~ G(x))
(d) $x ~ (F(x) & G(x))
(e) "x ~ (F(x) ® G(x))
(f) ~ $x ~ (F(x) & G(x))
(g) ~"x(F(x) & G(x))
14. Dado el siguiente enunciado, donde C está por ‘chica, G por ‘gustar’ y a se refiere a Arturo.
~$x(G(x) & L(a, x))
(a) Dar una interpretación que haga verdadero al enunciado
(b) Dar una interpretación que haga falso el enunciado
15. Dada la siguiente interpretación
a= Arturo
b= Bartolo
c= Clara
d= Doris
B ‘chico’: {a, b}
G ‘chica’: {c, d}
L ‘amar’
¿Qué enunciados de entre los siguientes son verdaderos y cuáles falsos?
(a) G(a)
(b) "x L(a, b)
(c) ~ L(a, d) Ú ~ B (d)
(d) ~ $x G(x)
(e) "x L(x, x)
(f) $x "x ((B (x) & G(y)) ® L(x, y))
(g) "x "y ((B (x) & G (y)) ® L(x, y))
(h) "x "y"z ((L(x, y) & L(y, z)) ® L(x, z)
16. Dada la siguiente interpretación
a= Alberto
b= Bartolo
c= Cecilio
H ‘caballo’: {b, c}
L ‘lugar’: {<a, b> <c, b> <b, b> <b, a>}
(a) Dar un enunciado falso en esta interpretación
(b) Dar un enunciado con una negación que sea verdadero en esta interpretación
(c) Dar un enunciado cuantificado universalmente que sea verdadero en la interpretación
(d) Dar un enunciado cuantificado existencialmente que sea falso en la interpretación
(e) Dar un enunciado con un cuantor existencial y uno universal que sea verdadero en la interpretación
17. Dar una interpretación que haga verdaderos todos los enunciados del ejercicio (1).